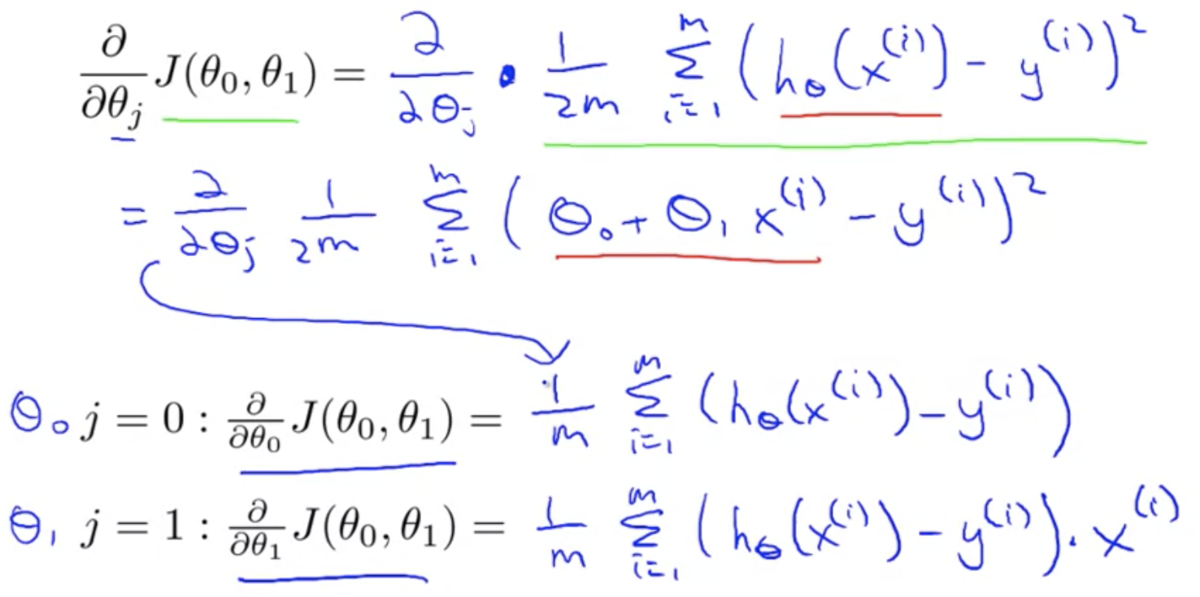第5週:ニューラルネットワーク:学習【Coursera Machine Learningコース】
Cost Function and Backpropagation
Cost Function
シンボル定義:
L ... ネットワーク内のレイヤー数
... レイヤー
にあるユニット数 (バイアスユニットは除く)
K ... 分類問題のクラス数
2クラス分類なら ,
,
多クラス分類なら ,
(K ≧ 3)
ロジスティック回帰のときのコスト関数は以下。
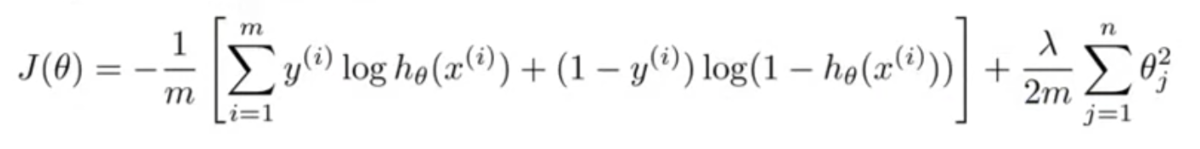
ニューラルネットワークでは以下のようになる。
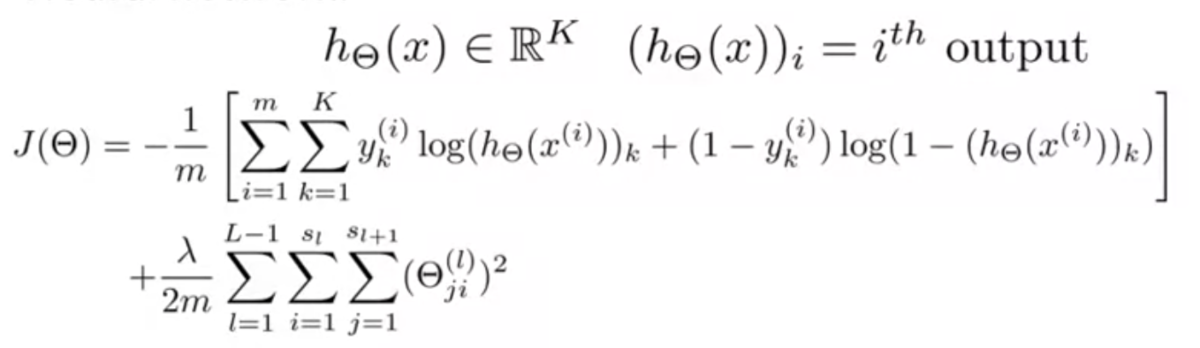
はユニットがK個あるうちの何番目かを表す添字。
ロジスティック回帰のコスト関数との違いは、ユニットK個分の和をとっていること。
正則化項はぱっと見複雑に見えるが、そんなに難しくない。
,
,
はそれぞれ、
層目の
番目のユニットの
番目の特徴量の重みを取り出すために使われている。
つまり、ネットワーク全体の重みの二乗和をとっているということ。
Backpropagation Algorithm
ニューラルネットワークでも、これまで同様、コスト関数とその微分が必要。
つまり、 の他に、
が必要。
この微分計算のために誤差逆伝搬法(Backpropagation)を使う。
誤差逆伝搬法は、レイヤ にあるノード
番目の誤差
を求めるイメージ。
ニューラルネットワークでは各レイヤにアクティベーション が存在するが、
このアクティベーションが、期待される値からどれだけずれているかを求めていく。
具体的には以下のような計算をする。
レイヤ で、トレーニングセットx, yがそれぞれ1つずつしかない場合を考えると
出力層 :
隠れ層 :
隠れ層 :
上式の ,
,
,
,
はそれぞれベクトル。
という演算子は、要素ごとの積を表している。
というのは、アクティベーション関数の
を入力値が
のところで微分した値。
これを計算すると、 になる。
なお、レイヤ1(入力層)にはアクティベーションがない(入力値)ので、 も存在しない。
このように、誤差 を出力層から始めてレイヤを遡りながら
計算していくので、誤差逆伝搬法と呼ばれている。
正規化項を無視すると、これらの誤差 を使って、
は以下のように計算できる。
以上の計算を、トレーニングセットが複数ある場合({(,
), ..., (
,
)})で考える。
まず、 とおく。これは後ほど偏微分項を累積するために使う。
次に から
までのループの中で(つまり各トレーニングセットに対して)以下の計算をする。
・(入力層)
・フォワードプロパゲーションにより を算出 (
)
・出力層の誤差 を計算
・バックプロパゲーションにより を計算
・ で偏微分項を累積する
最後に、ループを抜けたのち、以下のように正規化項の計算をする。
・(
の場合)
・(
, つまりバイアス項の場合)
以上で、ニューラルネットワークのコスト関数の偏微分は次のように計算できる。
Backpropagation Intuition
逆伝搬は線形回帰やロジスティック回帰に比べると、数学的にクリーンでもシンプルでもない。
なので直感的には理解しにくいかもしれない。
直感的に理解できなくても、使い方さえ覚えれば問題ない。
課題をこなすことで、逆伝搬の実装方法は分かるようになる。ひとまずそれでいい。
下図のようなニューラルネットワークがあるとする。
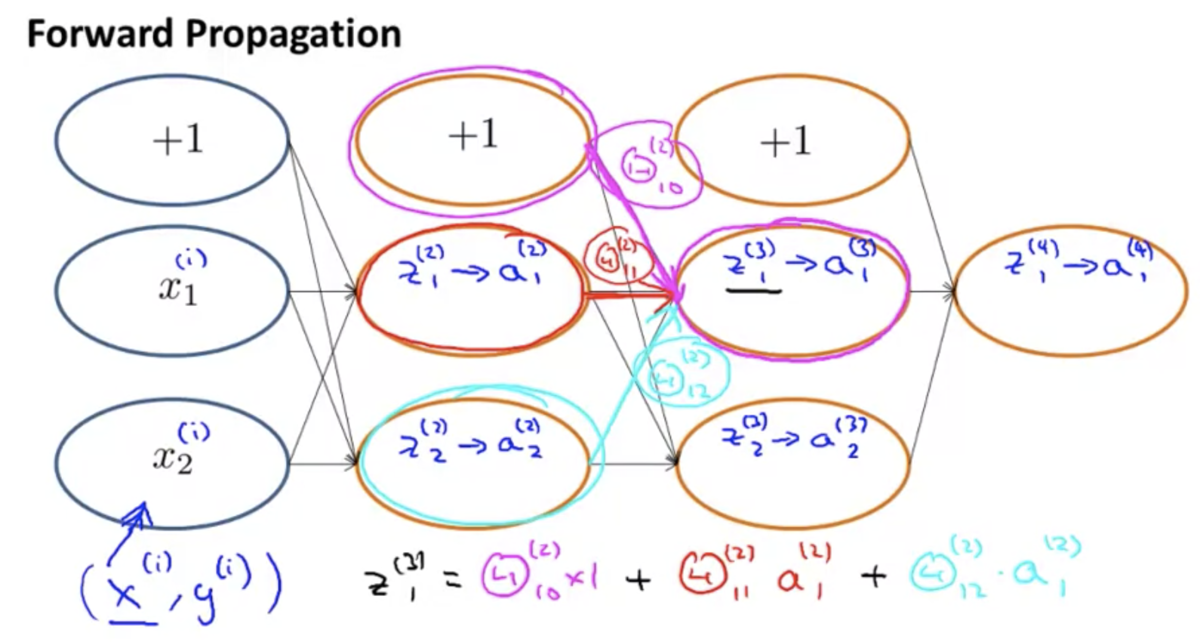
順伝搬において、あるノードへの入力は、ひとつ前のレイヤーの各ノードの出力に重みをかけたものの和になっている。
逆伝搬の計算も、これと似たプロセスになっている。
違いは、計算が左から右に流れるか、右から左に流れるか。
逆伝搬のコスト関数について、データセットのうち と
だけに着目し、出力ユニットはひとつだけとして、正規化項を無視すると、以下のようになる。
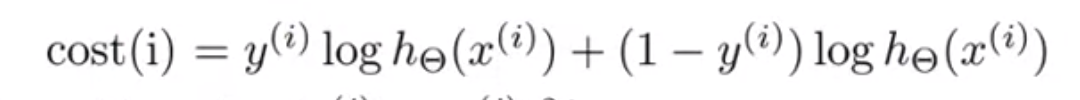
このコスト関数がやっているのは、誤差の2乗と似たような役割。
そのため、感覚的な理解としては、
のように近似して考えてもよい。
では、これを前提として、逆伝搬が何をやっているか。
逆伝搬は、 を計算している。
これは、 番目のレイヤーにある
番目のユニットのアクティベーション
の値の「誤差」と捉えることができる。
正式には、 を計算している。
直感的には以下のように理解すればよい。
の求め方は順伝搬とよく似ていて、前のレイヤーの各ユニットの誤差の重みつき和になっている。
例えば下図のように、出力層の誤差 は、正解データと出力値の差をとる。
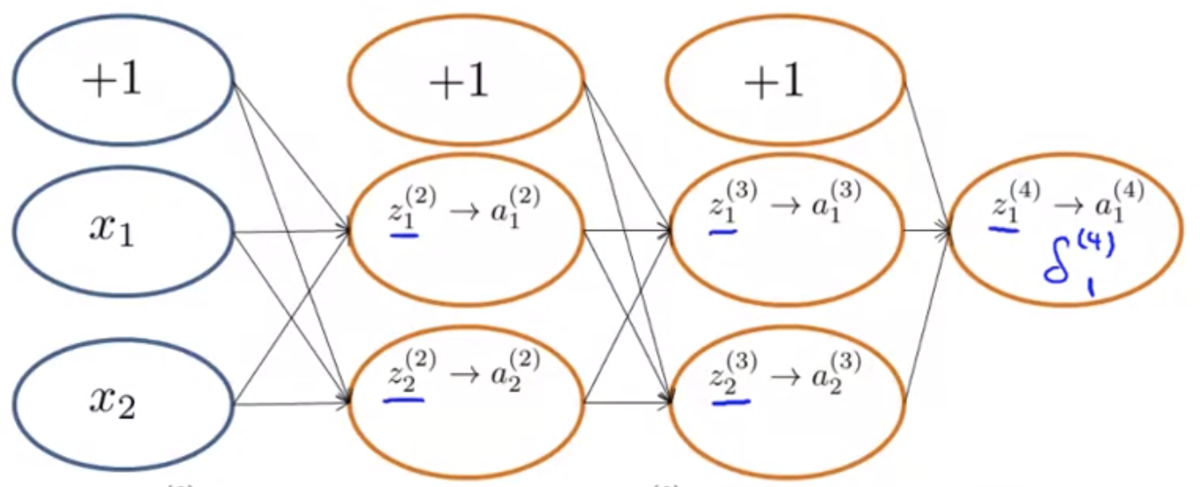
レイヤー2のユニット2の誤差 なら、下図のようになる。
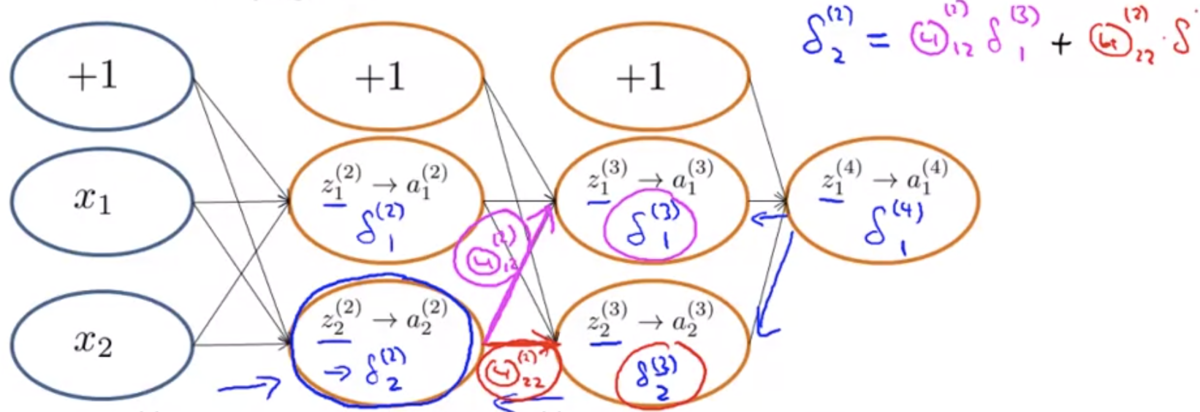
バイアスユニットについては誤差がないので無視してよい。
Backpropagation in Practice
Implementation Note: Unrolling Parameters
行列からベクトルへのパラメータのアンロールについて。
高度な最適化アルゴリズムを利用する際、これが必要になる。
Octaveで学習を走らせる際、以下のようなコードを書いてた。
function [jVal, gradient] = costFunction(theta) ... optTheta = fminunc(@costFunction, initialTheta, options)
ここで、thetaやgradientはベクトルを期待している。
しかしニューラルネットワークにおいてこれらは行列になる。
そのため、行列からベクトルへのアンロールが必要になる。
例として、下図のようなネットワークを考える。
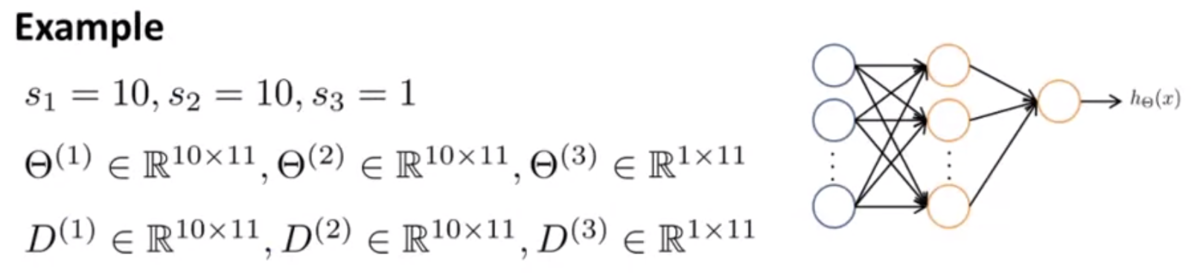
このとき、行列ΘやDをベクトルにアンロールするには、(Octaveの場合)以下のようなコードを書けばよい。

反対に、ベクトルを行列に戻す場合は以下のようなコードを書く。

Gradient Checking
逆伝搬の実装は複雑でバグが混入しやすい。
そして一見すると正しく動いているように見えてしまう。
この問題は、Gradient Checkingと呼ばれるアイデアで対処可能。
これは、別の方法で勾配(あるいはその近似値)を計算して、両者を比較することで正しさを検証するというもの。
勾配の近似値は下図のような式で求めることができる。
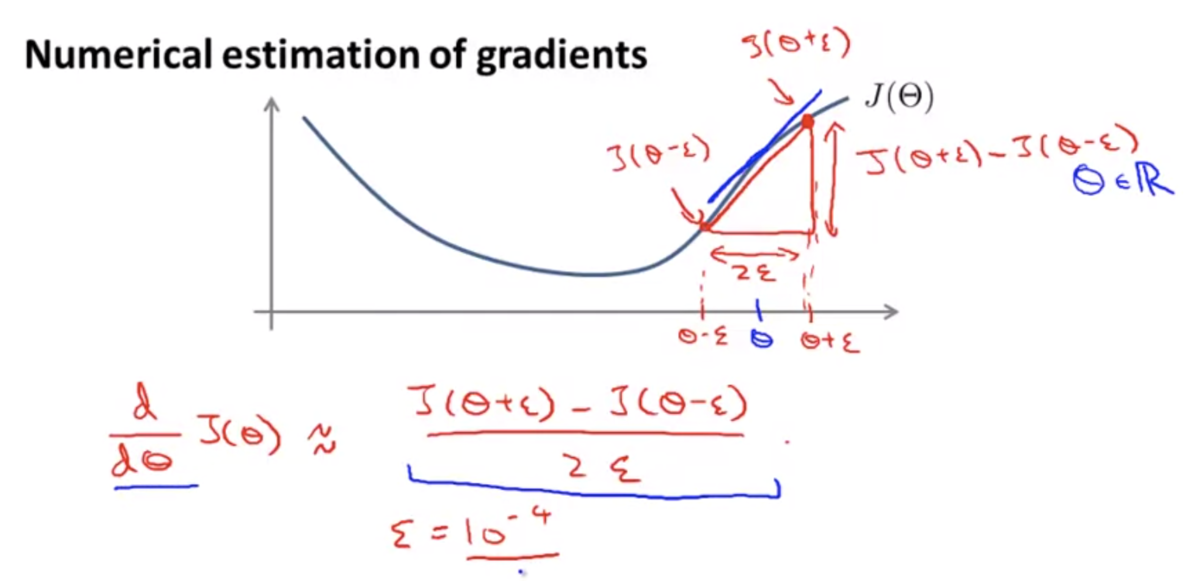
ある程度小さなεを設定し、これを使ってΘを両側微分したものを近似値として利用する。
Octaveで実装すると以下のようなコードになる。

Θをベクトルに拡張すると次のようになる。

Octaveで実装した場合こうなる。

得られたgradApproxと逆伝搬の計算で得られたDVecを比較し、差がある範囲に収まれば、逆伝搬の計算は正しい可能性が高くなる。
なお、Gradient Checkingは逆伝搬の実装を検証する際にのみ使用し、実際に学習する際にはいちいち計算しないように注意する。
逆伝搬の計算と比較して計算に時間がかかるので、この方法を使って学習することはしない。
Random Initialization
Random Initializationと呼ばれるアイデアについて。
学習のために最適化アルゴリズムを走らせる際、パラメータΘの初期値を選ぶ必要がある。
ロジスティック回帰の場合は、ゼロ初期化でうまくいった。
しかしニューラルネットワークの場合、Θをゼロ初期化するとうまく動かない。
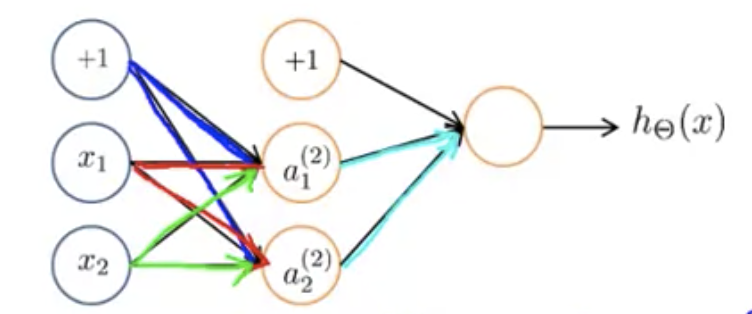
そのため、Θをランダムに初期化する必要がある。
Θを の範囲の値で初期化するために、Octaveでは以下のように記述すればよい。
Theta1 = rand(10, 11) * (2 * INIT_EPSILON) - INIT_EPSILON; Theta2 = rand(1, 11) * (2 * INIT_EPSILON) - INIT_EPSILON;
rand(10, 11)は10x11の0から1の間の値をとる行列を生成する。
Putting It Together
ニューラルネットワークの利用手順について。
● モデル形状の決定
- 入力層のユニット数 ... 扱う特徴量の数できまる
- 出力層のユニット数 ... 分類に必要なクラスの数できまる
- 隠れ層の数 ... 通常は1層でいい
- 隠れ層のユニット数 ... だいたい入力層のユニット数と同程度 ~ 4倍程度にする 隠れ層が複数あるなら各層のユニット数は同じにする
● 学習の実装
- パラメータΘをランダムに初期化する (Θは0付近の値)
- フォワードプロパゲーションを実装して
に対する
を計算可能にする
- コスト関数
の実装
- バックプロパゲーションを実装して偏微分
を計算可能にする
- バックプロパゲーションの実装の正しさを検証するためにGradient Checkingを行う (検証が済んだらこの処理はOFFにしておく)
- 勾配降下法、またはより高度な最適化アルゴリズムによって
を最小化する処理を実装する
Application of Neural Networks
Autonomous Driving
ニューラルネットワークで自動運転する研究結果の映像。
第4週:ニューラルネットワーク:表現【Coursera Machine Learningコース】
Motivations
Non-linear Hypotheses
なぜニューラルネットワークが必要なのか?
下図のようなデータセットの分布の分類問題を解きたいとする。
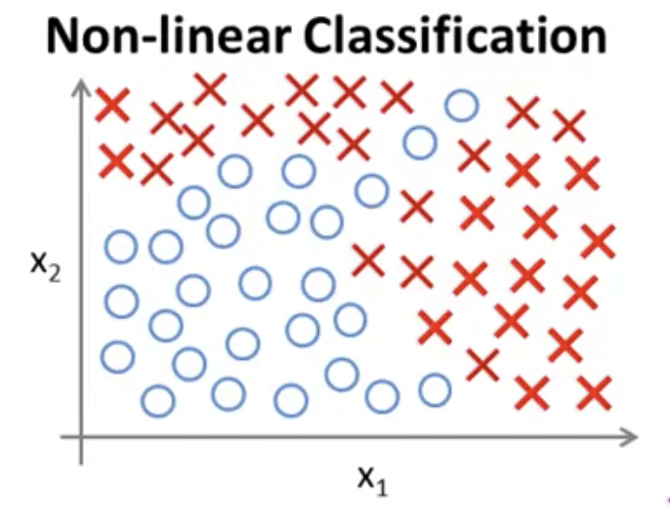
このデータセットに仮説をフィットさせるには、非線形な仮説にするために、
次数の高い多項式にする必要があった。
しかしこのとき、特徴量の種類が多い場合、多項式がとても複雑になる。
例えば特徴量が100個ある場合、2次式を作ろうとすると、
2次の項だけ数えても、項の数は5000個ほどになる。
(,
, ... ,
, ... ,
)
これはオーバーフィッティングを招いてしまう。
また、計算量はほどと、とても高コストになる。
例えば画像処理では、各ピクセルの画素値が特徴量として用いられる。
仮に50 x 50ピクセルの画像だったとしても、特徴量は2500個と膨大になる。
RGB画像であればさらに3倍の7500個になる。
このような問題にロジスティクス回帰は向かない。
Neurons and the Brain
ニューラルネットワークの概要。
ニューラルネットワークは脳の模倣を目指したアルゴリズム。
80年代〜90年代によく使われていた。
計算コストが高い等の理由で使われなくなっていたが、近年また注目を集めている。
人間の脳は、ひとつのアルゴリズムで学習を行っているという仮説があるらしい。
例えば耳の情報を処理する聴覚皮質という部位を視神経とつなげると、
視覚情報を処理できるようになるという研究結果があるという。
他にも額につけたカメラの映像を舌で処理する研究や、 カエルに3番目の目を取り付けると
その情報を処理できるようになるという研究結果などがあるとのこと。
このように柔軟に学習する脳の仕組みををコンピュータに実装できれば、
真に知能をもった人工知能を作れるのではないか、というのが根っこにあるアイデア。
Neural Networks
Model Representation 1
脳はニューロンと呼ばれる細胞で構成されている。
ニューロンの細胞体からは、dendrite(樹状突起)と呼ばれる入力部が複数伸びている。
これらを介して他のニューロンから信号を受け取る。
信号を受け取ったあと、内部で何らかの処理を行い、
axon(軸索)と呼ばれる出力部から他のニューロンへ信号を送り出す。
情報伝達は微弱な電気信号(スパイク)をやりとりして行う。
この仕組みをモデル化したものが以下の図。
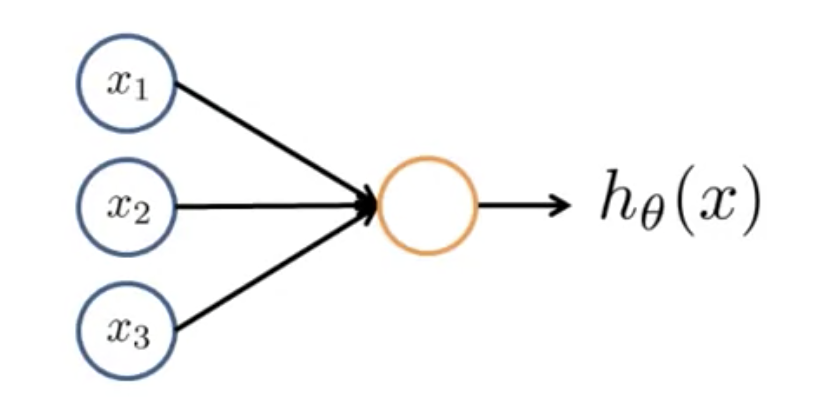
黄色い円がニューロン本体。
,
,
が入力で、黄色い円と入力をつなぐ矢印がdendriteにあたる。
ニューロンは入力を受け取ったあと、計算を行い、なんらかの値を出力する。
出力側の矢印がaxonにあたる。
は、
ニューラルネットワークにおいては、このシグモイド関数を
「活性化関数(activation function)」と呼んだりする。
x, θに関してはこれまで同様パラメータベクトルを表している。
ニューラルネットワークにおいては、θを「重み(weight)」と呼ぶこともある。
ニューラルネットワークを図示する場合、分かりやすさのために、
下図のように追加のノードを書き加えることもある。
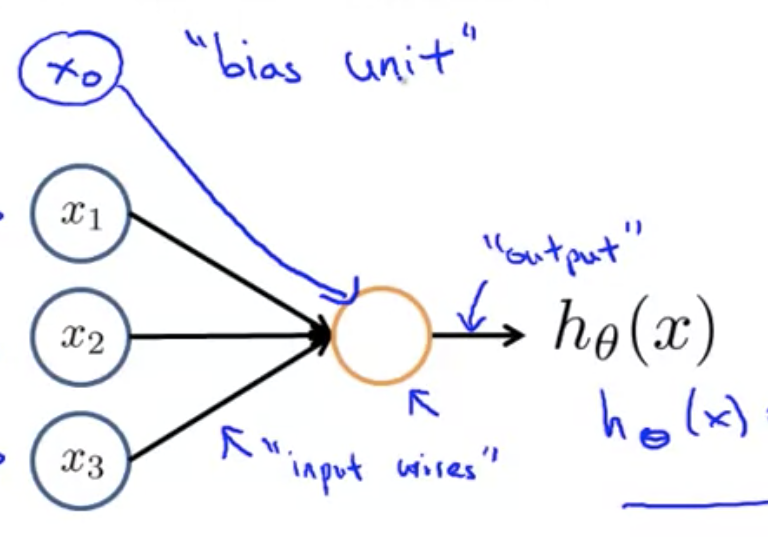
このノードを「バイアスユニット」や「バイアスニューロン」と呼ぶ。
の値は1なので、理由がなければ書かなくてもよい。
ニューラルネットワークとは、下図のように、上記のようなモデルがいくつか集まったもののこと。
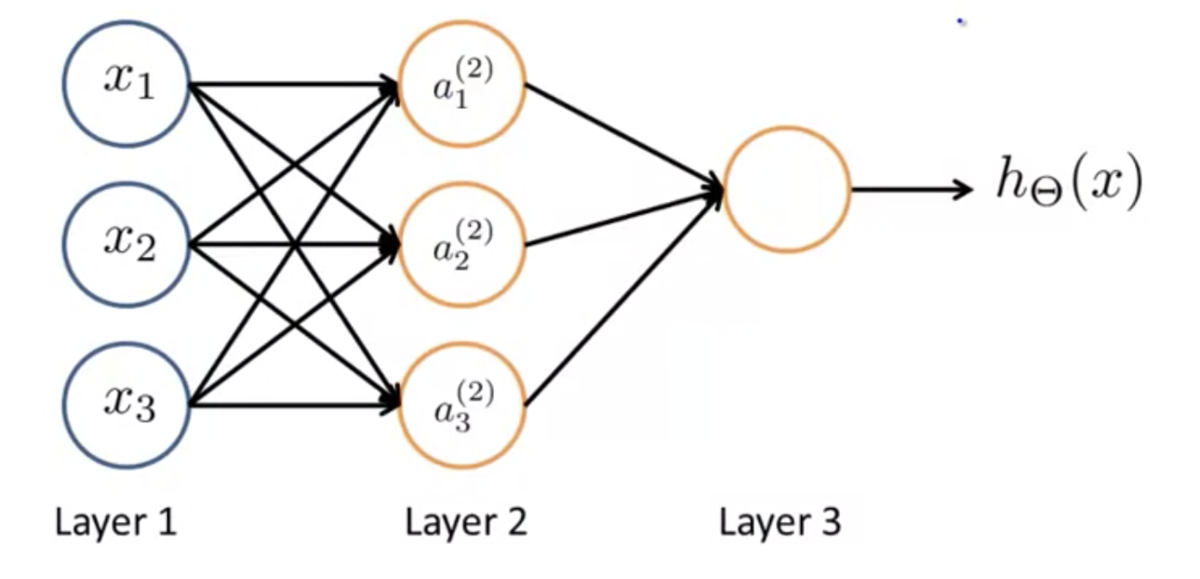
Layer 1 を「入力層(Input Layer)」、Layer 3を「出力層(Output Layer)」と呼ぶ。
また、入力層と出力層に挟まれたレイヤーを「隠れ層(Hidden Layer)」と呼ぶ。
外から直接観測することができないためこう呼ばれる。
隠れ層は1つとは限らず、入力層でも出力層でもない層はなんでも隠れ層と呼ぶ。
シンボル定義について。
を、レイヤー
のユニット
の「アクティベーション」と呼ぶ。
アクティベーションという言葉は、別のレイヤーの計算結果の値、つまり出力値を指している。
は、レイヤー
からレイヤー
へマッピングする関数を制御する重みを表すパラメータ行列。
上図では、以下のような計算が行われていることになる。
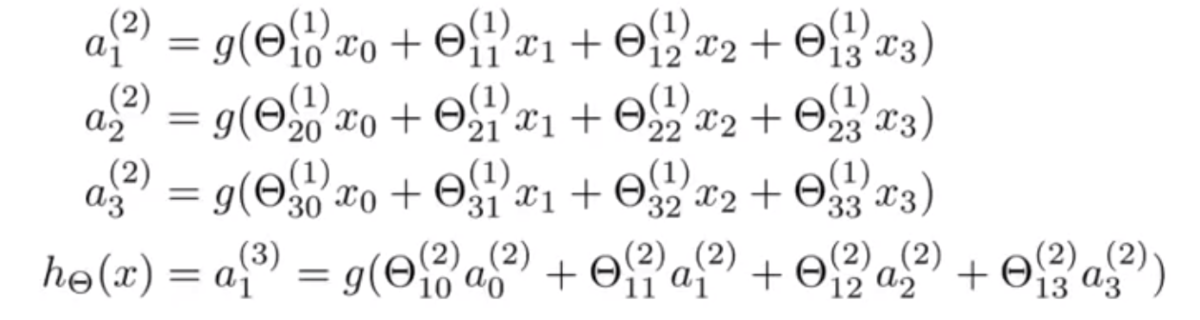
もしネットワークがレイヤー にユニットを
個もち、
レイヤー にユニットを
個もつなら、
の次元は
になる。
たとえばレイヤー 1 にユニットが 2 個、レイヤー 2 にユニットが 4 個あるなら、Θ の次元はになる。
Model Representation 2
計算の効率化(ベクトル化)について。
とおくと、
と書くことができる。
他の多項式も同様にして ,
とおくと、
ニューラルネットワークで行われる計算を以下のようにベクトルで表現できる。
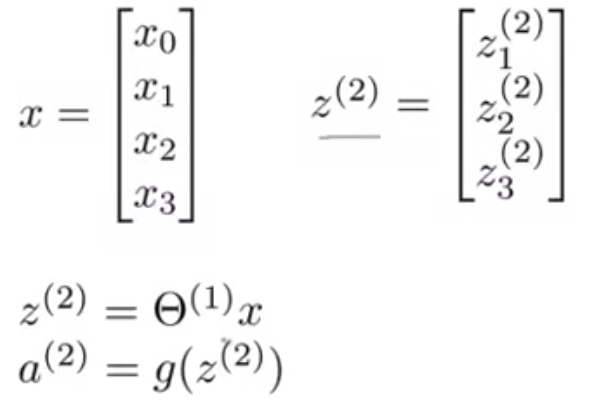
また、記述の一貫性をもたせるために、入力層のxについて、[tex:a ^ {(1)} = x}と定義する。
(入力レイヤーのアクティベーションとして解釈する)
つまり、
出力層についても同様に、
とおくと、
と書ける。
ただし、ここで は隠れ層のバイアスユニットで、
この を得るまでの一連の処理を、フォワードプロパゲーションと呼ぶ。
入力層のアクティベーションから始めて、隠れ層を経て、出力層へ、というふうに、
計算を前方(フォワード)へ伝搬(プロパゲーション)させていることによる。
なぜこのニューラルネットワークのアイデアが効果的なのか。
次のようなニューラルネットワークについて考える。
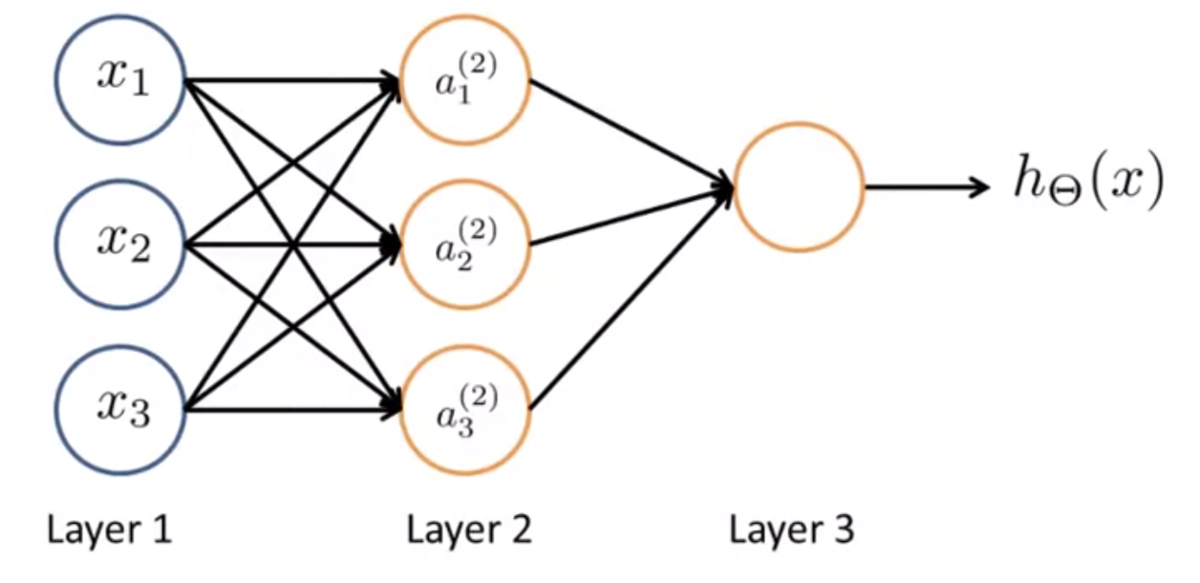
下図のように、入力層の部分を隠してみる。
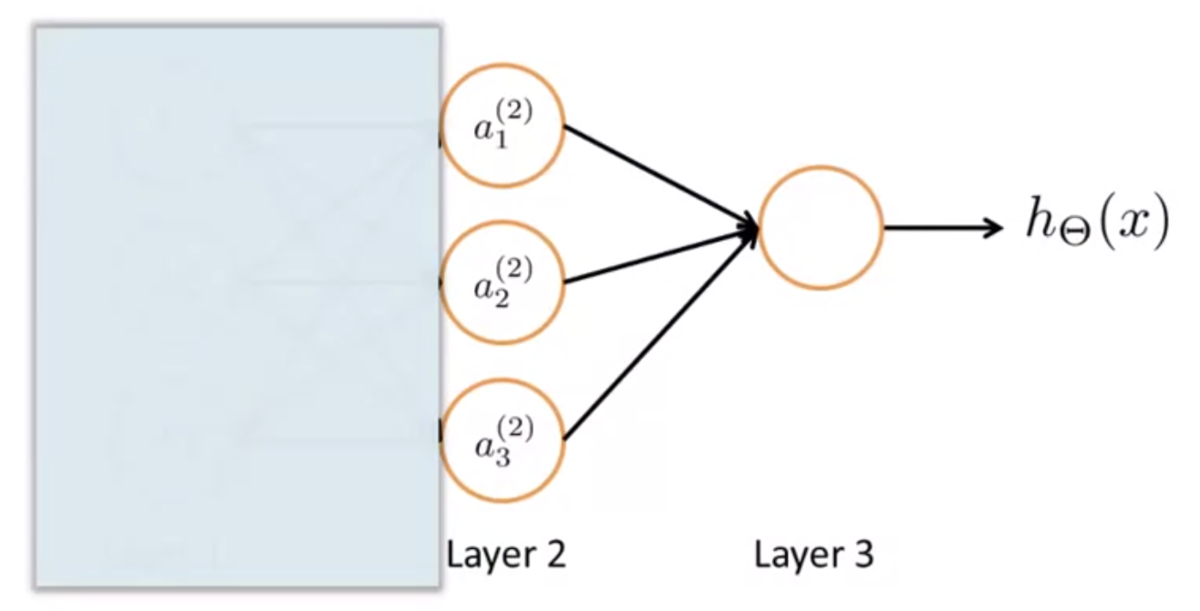
すると、このネットワークで行われる計算は単純なロジスティック関数になる。
ロジスティック回帰との違いは、特徴量として、 ではなく
を使うという点。
は、それ自身が学習結果であり、
で定義されている。
によって多様な表現ができるので、特徴量xをそのまま使ったり、
xの組み合わせで作られた多項式の中からひとつを選ぶよりも、よりよい仮説を得られる。
Applications
Examples and Intuitions 1
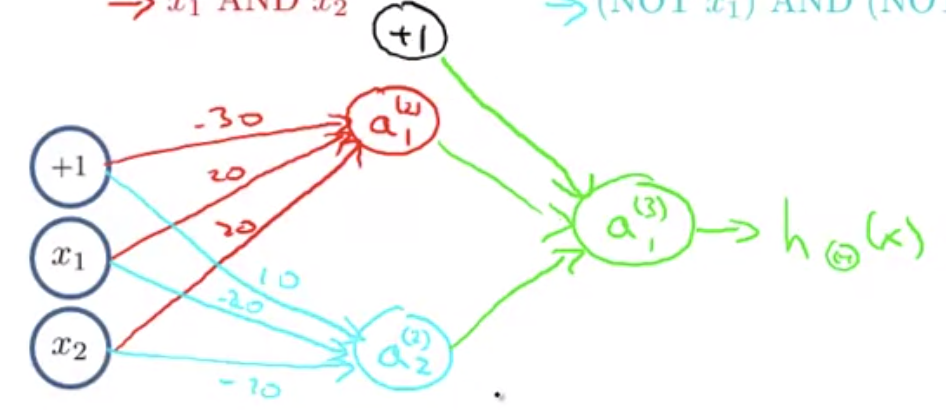
ニューラルネットワークはパラメータの組み合わせによってAND・OR関数を表現可能。
ANDの例
とする
,
,
とすると、
となる
このネットワークの出力を表にすると以下のようになる
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
ANDを表していることがわかる
ORの例
とする
,
,
とすると、
となる
このネットワークの出力を表にすると以下のようになる
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
ORを表していることがわかる
Examples and Intuitions 2
他にも、NOTも表現可能。また、AND・OR・NOTを組み合わせてXNORを作れる。
NOT
入力としてバイアスユニットと[ tex:x _ 1] があるとする。
とする
,
とすると、
となる
このネットワークの出力を表にすると以下のようになる
| 0 | |
| 1 |
NOTを表していることがわかる
XNOR
AND・(NOT A)AND(NOT B)・ORの3組のニューロンを作る
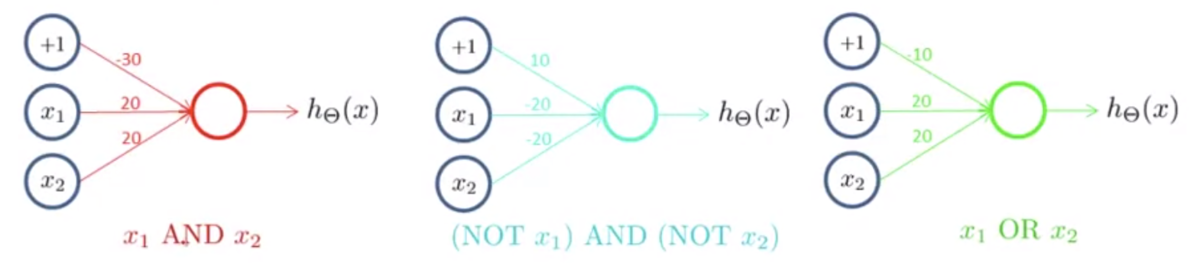
下図のように組み合わせる
真理値表は次のようになる
| 0 0 | 0 1 | 1 |
| 0 1 | 0 0 | 0 |
| 1 0 | 0 0 | 0 |
| 1 1 | 1 0 | 1 |
XNORを表していることがわかる
XNORは下図のようなプロットの決定境界を表現できる
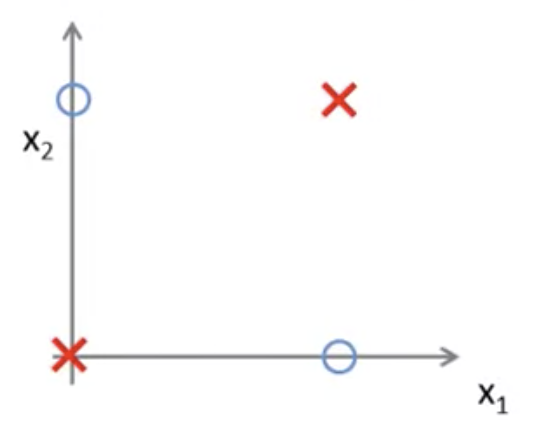
これができると、次のような非線形な決定境界も表現できることになる
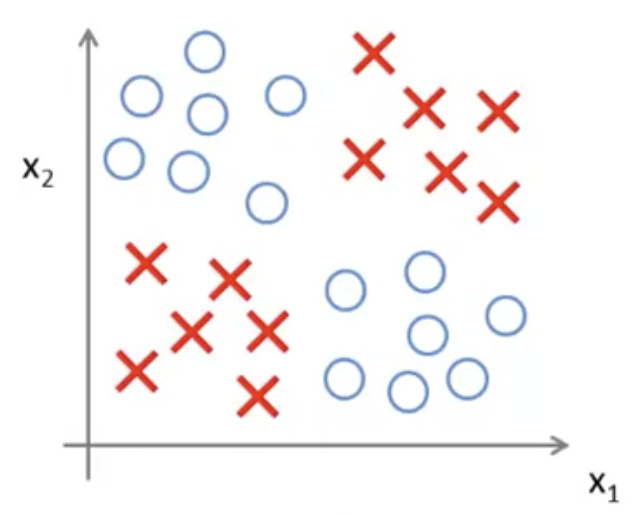
このように、ニューロンの組み合わせにより複雑で非線形な仮説を得ることができる
Multiclass Classification
ニューラルネットワークで多クラス分類をするには、出力層に複数のユニットをおく。
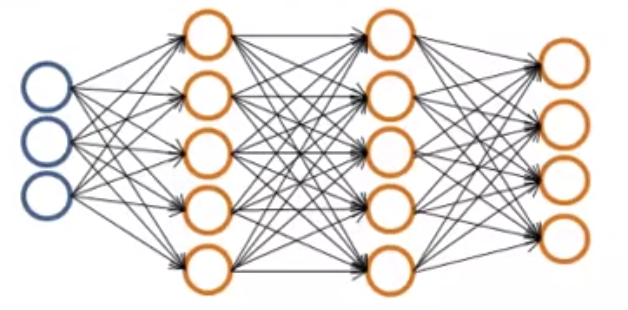
そして、各ユニットに、あるクラスがYesかNoかを判別させる
画像認識を例にすると、1つめのユニットは歩行者か否かを判別し、
2つめのユニットは車か否かを判別し...というような具合
各ユニットの出力はクラス数の次元のベクトルで、
例えば4クラス分類なら出力は
,
,
,
のいずれかになる
これらは、ニューラルネットワークを使ってone vs allを再現しているような形になる
第3週:ロジスティック回帰【Coursera Machine Learningコース】
テーマ
分類と表現 (Classification and Representation)
分類 (Classification)
分類問題の例:

目的変数が0か1かで判別する

線形回帰ではデータをうまく2つに分けることができない
また、分類問題では or
であるべきなのに、
線形回帰の仮説では or
も有り得てしまう
そのため線形回帰は分類問題に適さない
仮説表現 (Hypothesis Representation)
どのような関数を仮説の表現に用いるか
分類問題では となるような仮説が欲しい
線形回帰の仮説の形は だった
ロジスティクス回帰では、 のような形になる
ここで は
と定義される
この関数はシグモイド関数、またはロジスティクス関数と呼ばれるもの
ロジスティクス関数は以下の図に示すように、 になる性質をもつ
そのため、分類問題に求められる仮説の条件を満たす
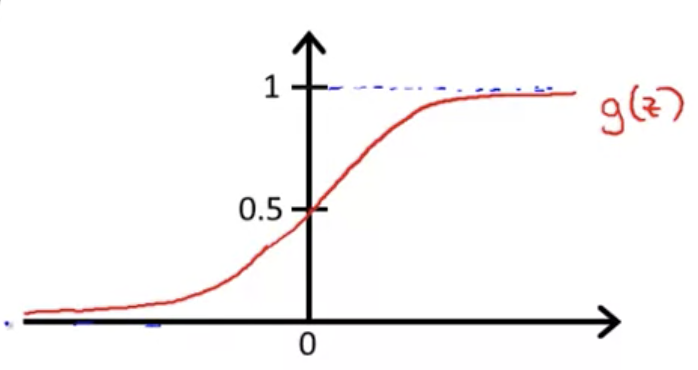
この に
を代入すると、
となる
これがロジスティクス回帰の仮説
仮説の出力の解釈について
ロジスティクス回帰の仮説 の出力は、
入力 に対する結果
が 1 になる確率を表している
例えば だったら、その入力
は70%の確率で 1 に分類されるということ
これを形式化すると次の式のように書ける
(θ でパラメータ化された x が与えられたときに y = 1 である確率、と読む)
決定境界 (Decision Boundary)
決定境界と呼ばれるものを知ることでロジスティクス回帰が何を計算しているかを理解する
のとき
のとき
とすると、ロジスティクス回帰では のとき必ず y = 1 となる (逆も成り立つ)
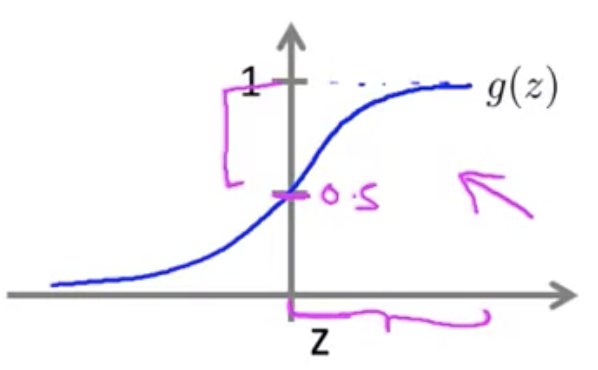
つまり、 なら
,
なら
となる
ここで、下図のようなデータセットの分布があったとする
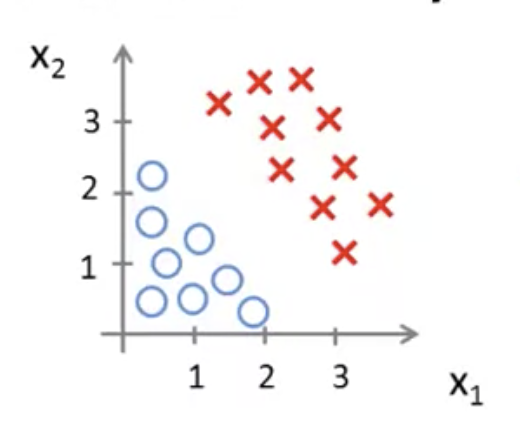
仮説として次のような式を用いる
このとき、最適なの値が
だったとする
ロジスティクス回帰では なら
なので、
この場合は
⇒ のとき
となる
という直線を図に加えると以下のようになる
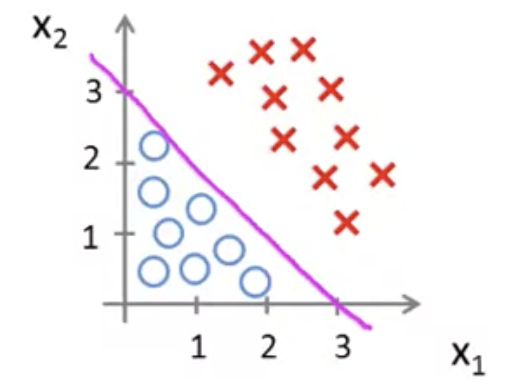
は直線の上の領域を表す
つまり y = 1となる領域
逆に、直線の下の領域は y = 0 の領域となる
このようにy = 1 の領域とy = 0の領域を分ける直線を決定境界と呼ぶ
なお、決定境界はデータセットの性質ではなく、仮説とパラメータの性質である
例としてデータセットの分布が以下の図のような場合、
のようにしておけば、
パラメータを適切に最適化することにより円の方程式を得ることができる
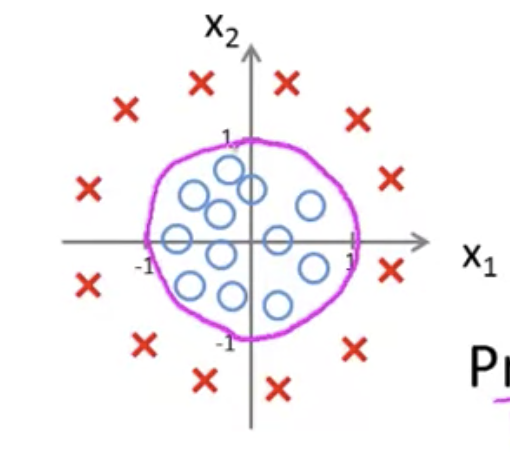
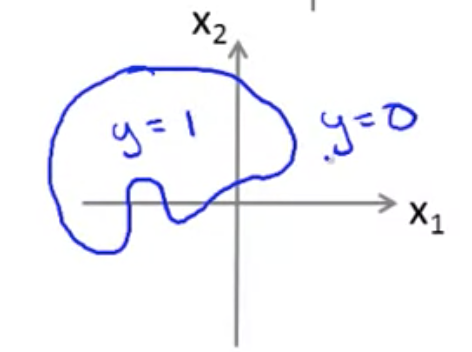
さらに高次の多項式では、より複雑な決定境界を得ることも可能
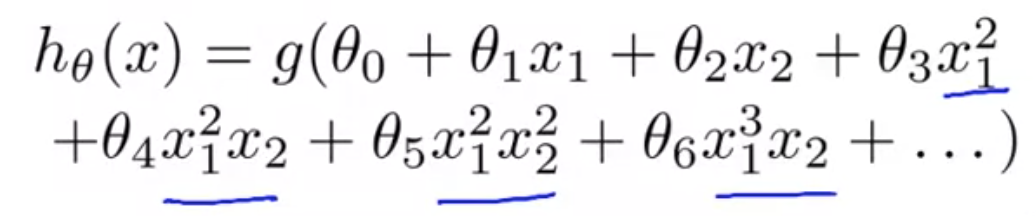
ロジスティック回帰モデル (Logistic Regression Model)
目的関数 (Cost Function)
今まで見てきたコスト関数を次のように変形する(1/2の場所を移動)
ここで、二乗誤差の項を次のようにおく
代入すると以下のようになる
は文字通り、学習アルゴリズムが値を出力する際、
予測が で実際のラベルが
だった場合に発生するコスト(費用)であると解釈する
線形回帰の場合は二乗誤差をコストとして用いることができたが、
ロジスティクス回帰の場合、二乗誤差を使うと目的関数は下図のように非凸関数になってしまい、
勾配降下法で最適解を求めることが困難になってしまう(勾配降下法は凸関数の場合に効果を発揮する)
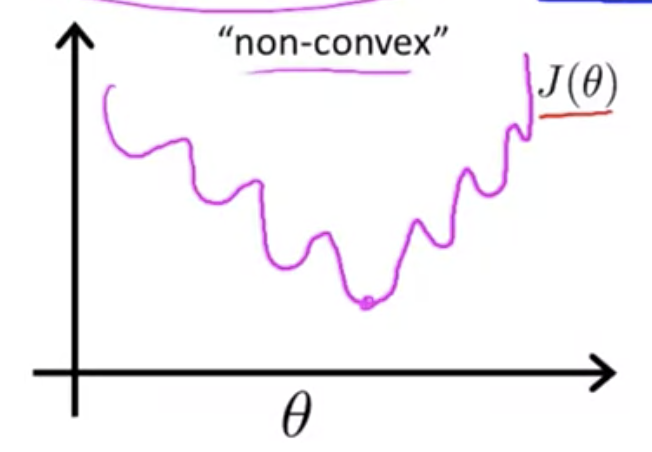
そこで、ロジスティクス回帰では次のようなコスト関数を用いる
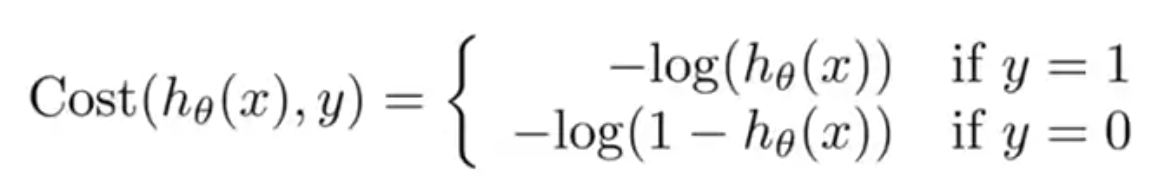
それぞれの関数では が
の範囲に収まるため、以下の図のようなプロットになる
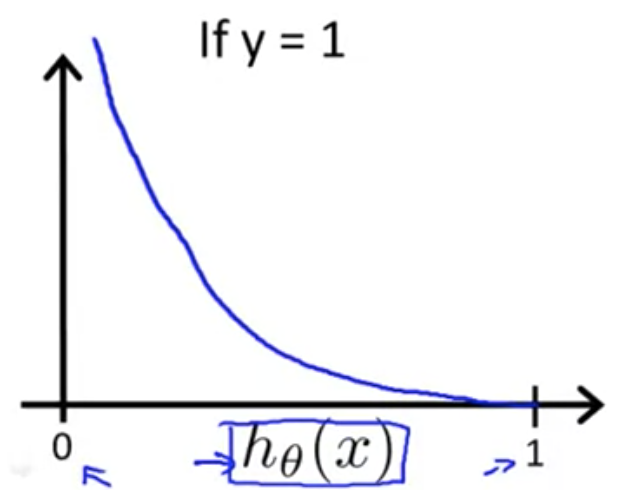
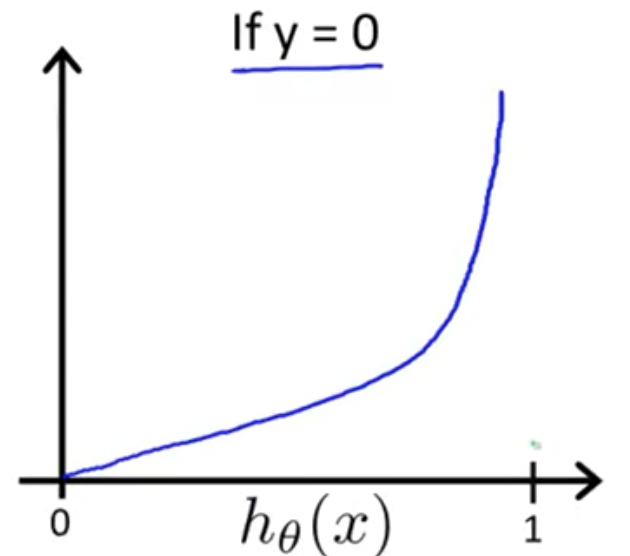
のときは
が 0 に近くほど、
また のときは
が 1 に近くほど、
コストが無限大に近づいていることがわかる
簡素化された目的関数と勾配降下法 (Simplified Cost Function and Gradient Descent)
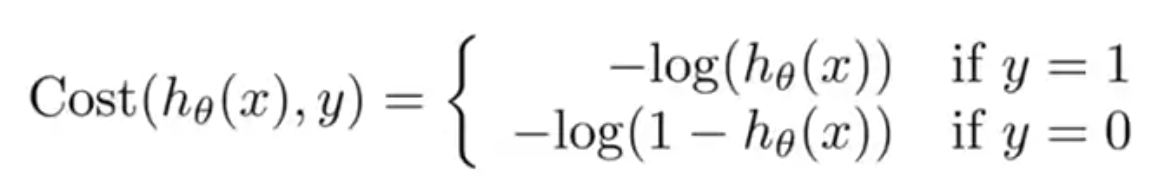
この式は、以下のように1行にまとめることができる
よって、ロジスティクス回帰の目的関数は以下のようになり、
パラメータ を最適化するにはこの
を最小化すればいい
を最小化には勾配降下法を用いる
勾配降下法のアルゴリズムは以下のようなもの
偏微分項を計算すると、線形回帰のときと同様の形になる
( はロジスティクス回帰のもの)
高度な最適化 (Advanced Optimization)
勾配降下法ではと
の偏微分を計算するが、
この2つを用いることで、別の(より高度な)最適化アルゴリズムも利用できる
- 共役勾配法 (Conjugate gradient)
- BFGS
- L-BFGS
これらに共通する特徴として、以下がある - 学習率αを手動で求める必要がない - 多くの場合、勾配降下法より高速
ただし、勾配降下法と比べて複雑なため、理解しようとすると難しい
これらを使うときは自前で実装するのではなく、機械学習ライブラリを使うべき
最適化手法のOctaveによる実装方法解説あり
Ovtaveのインデックスは1オリジンなので注意
多クラス分類 (Multiclass Classification)
one-vs-all (one-vs-rest) 分類というアルゴリズム →多クラス分類をいくつかの2クラス分類に分割して考える
例:クラスA, B, Cという3クラスに分類する問題 → 以下の3種類の2クラス分類に分割する ・クラスAとそれ以外の2クラス分類 ・クラスBとそれ以外の2クラス分類 ・クラスCとそれ以外の2クラス分類
実際に推測を行うときは、入力に対して、上記で得られた各分類器でそれぞれ推測を行い、もっとも確率の高い分類器の結果を返す
Solving the Problem of Overfitting
The Problem of Overfitting
オーバーフィッティング(過学習)問題とは
学習モデルが、データセットにはよく適合するが、データの予測には適さない状態になってしまうこと
このような状態をハイバリアンスとも表現する
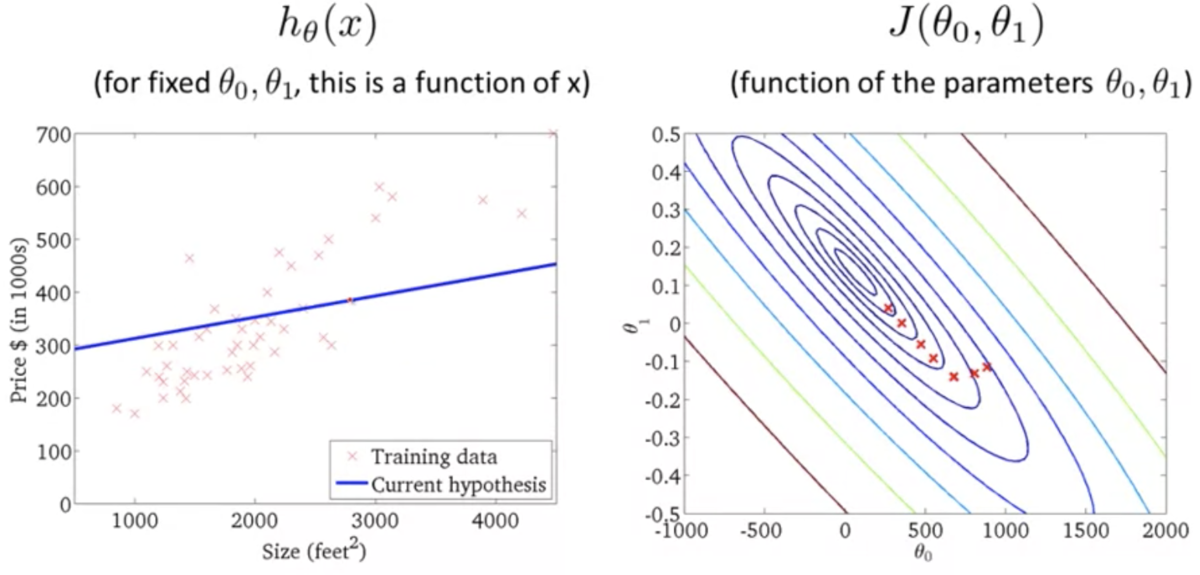
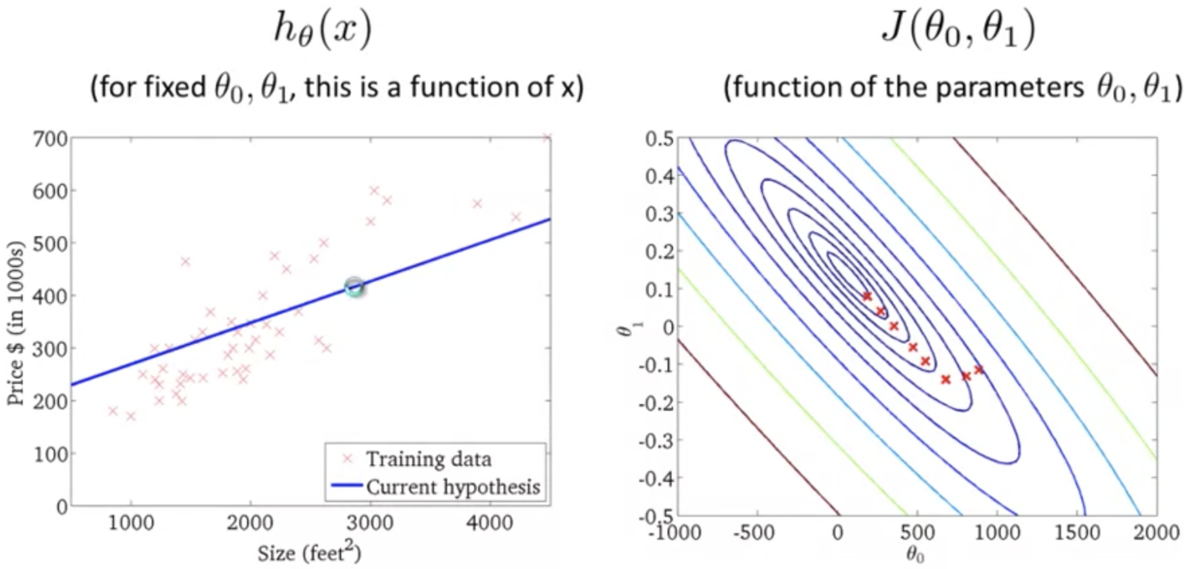
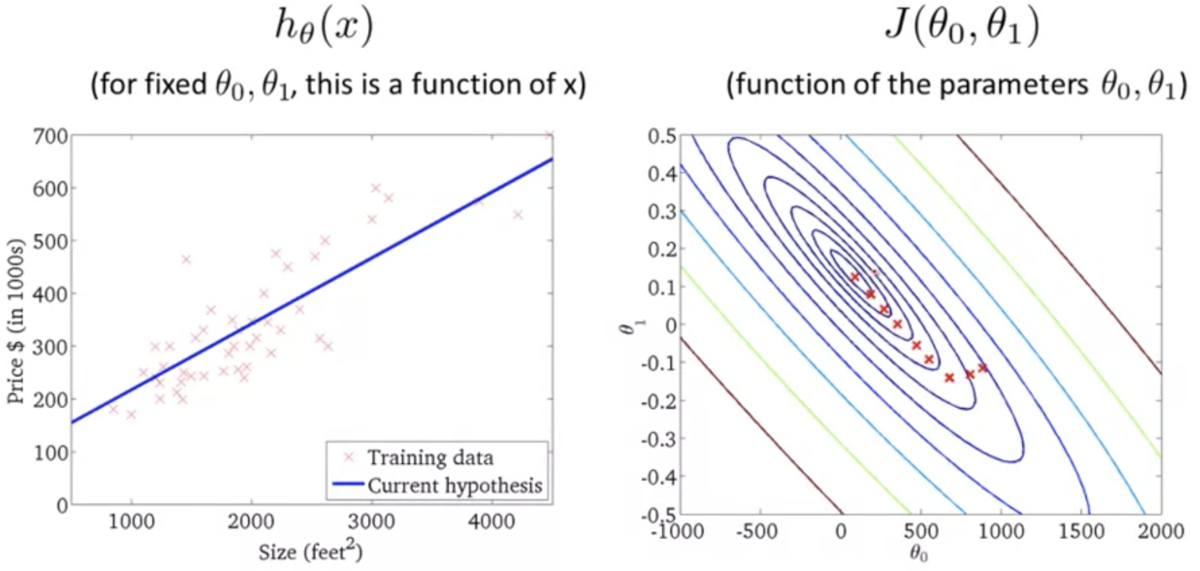
線形回帰の例(3枚目がオーバーフィッティング):
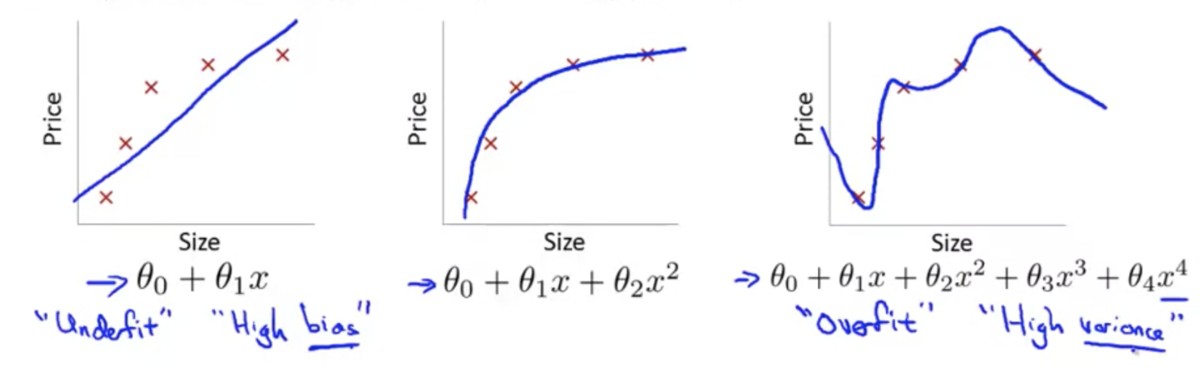
ロジスティック回帰の例(3枚目がオーバーフィッティング):
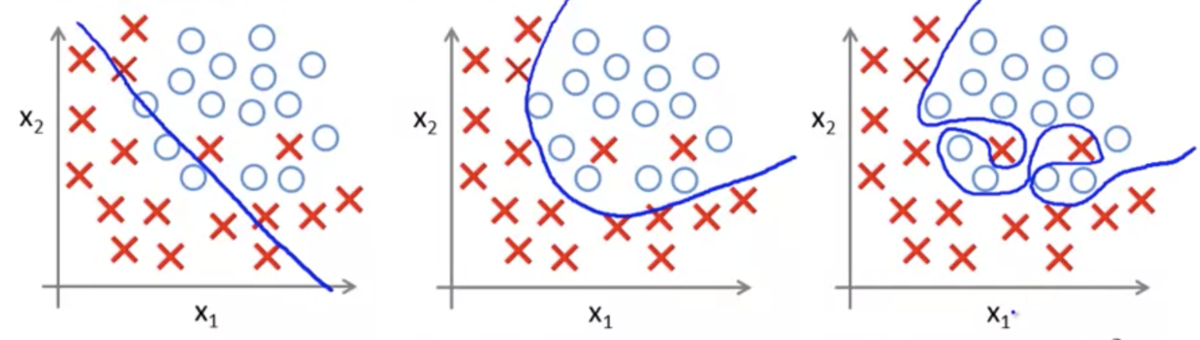
オーバーフィッティングが起きてしまったときの対応策
特徴量の種類を減らすデメリットとして、事前に重要な特徴量を知ることはできないため、重要な特徴量まで除外してしまう可能性があること
目的関数 (Cost Function)
パラメータθを小さく保つことで、よりシンプルな仮説となり、オーバーフィッティングしにくくなる
例えば下図のように、線形回帰の目的関数に正則化項を加えることで、θを小さく保つことができる→正則化
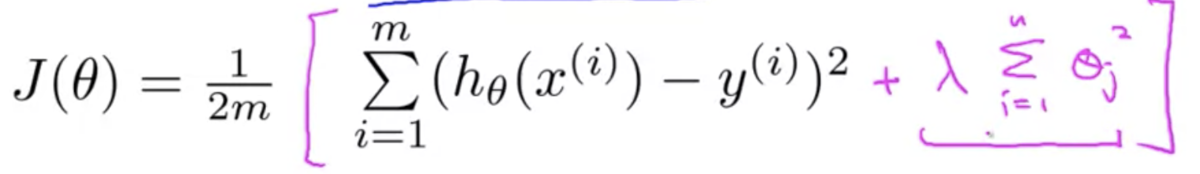
目的関数を最小化するには、正則化項が小さくなければならず、
正規化項を小さくするには、θを小さくしなけらばならない
→θを小さく保つことができる
ただし、正則化項のλがあまりに大きすぎると、各θはほぼゼロになる
すると、仮説が特徴量の影響をほぼ受けなくなってしまい、アンダーフィッティング状態に陥る
その場合、仮説はの形に近づき、プロットは下図のようになる

正則化された線形回帰 (Regularized Linear Regression)
正則化を取り入れた目的関数を勾配降下法で最適化する際は、以下のようにの場合とそれ以外とで場合分けをする
後者は正則化項が含まれた目的関数を偏微分しているので式の形が一部変わっている
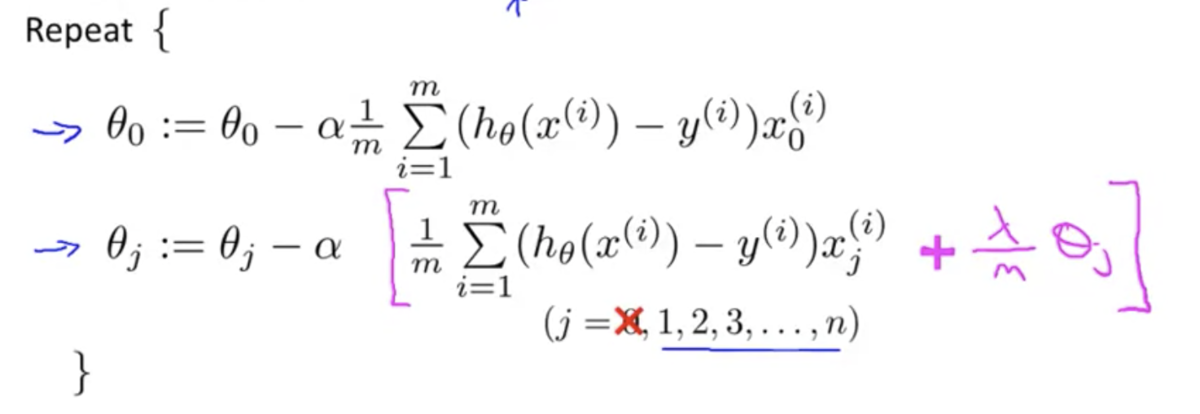
また、に関わる項をひとつにまとめると以下のようになる
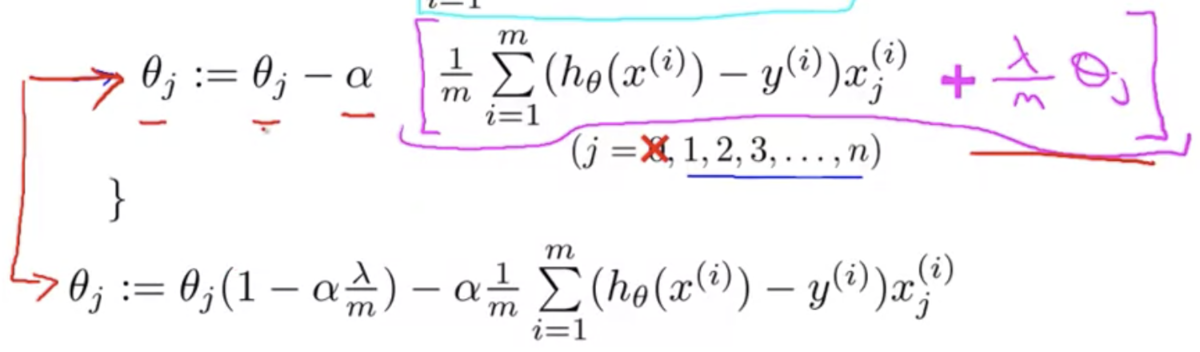
は通常 1 よりやや小さい値になる
なぜなら、学習率 α は正の小さな値を設定し、m は大きな値をとるから
1 より少しだけ小さい数字を に乗じるので、
の値は少しだけ小さくなる
なので、正則化項のある目的関数の勾配降下法では、各イテレーション毎に を少しだけ小さくし、あとは正則化項がない場合と同様のアップデートを施す
正規方程式の場合は、θ を求める式が以下のように変わる
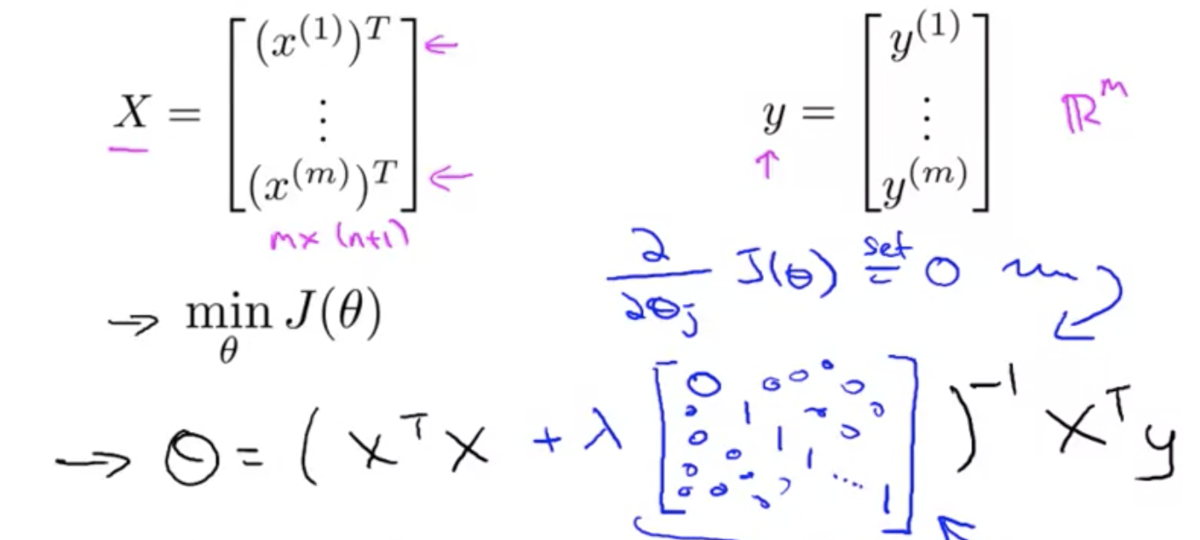
正則化されたロジスティック回帰 (Regularized Ligistic Regression)
ロジスティック回帰に正則化を適用する場合も、だいたいは線形回帰の場合と同じ
目的関数は以下のようになる
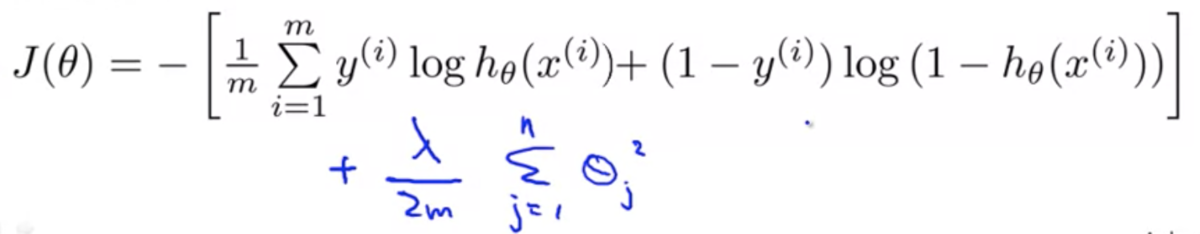
勾配降下法は以下のようになる
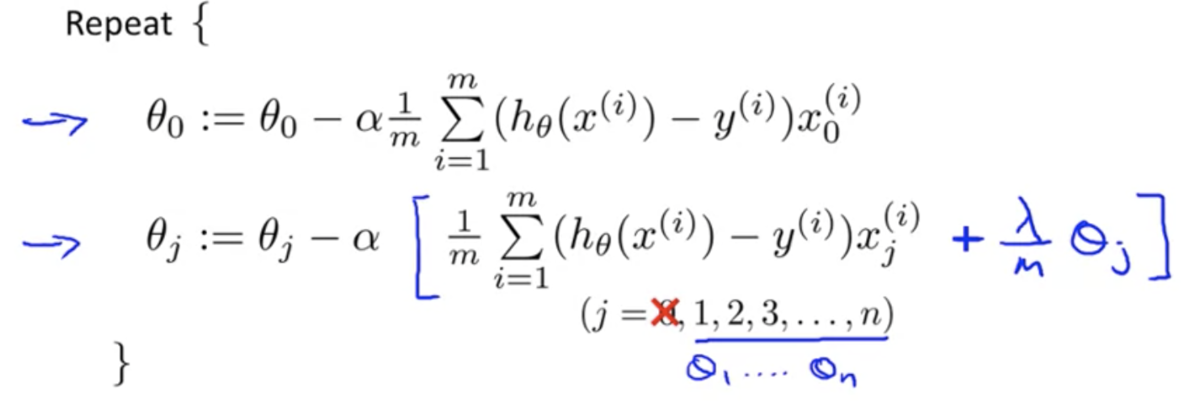
第2週:複数の変数を使用した線形回帰【Coursera Machine Learningコース】
プログラミング課題の環境構築
- Octaveをインストール
多変量線形回帰 (Multivariate Linear Regression)
複数の特徴量 (Multiple Features)
複数の特徴量を使う場合を考える
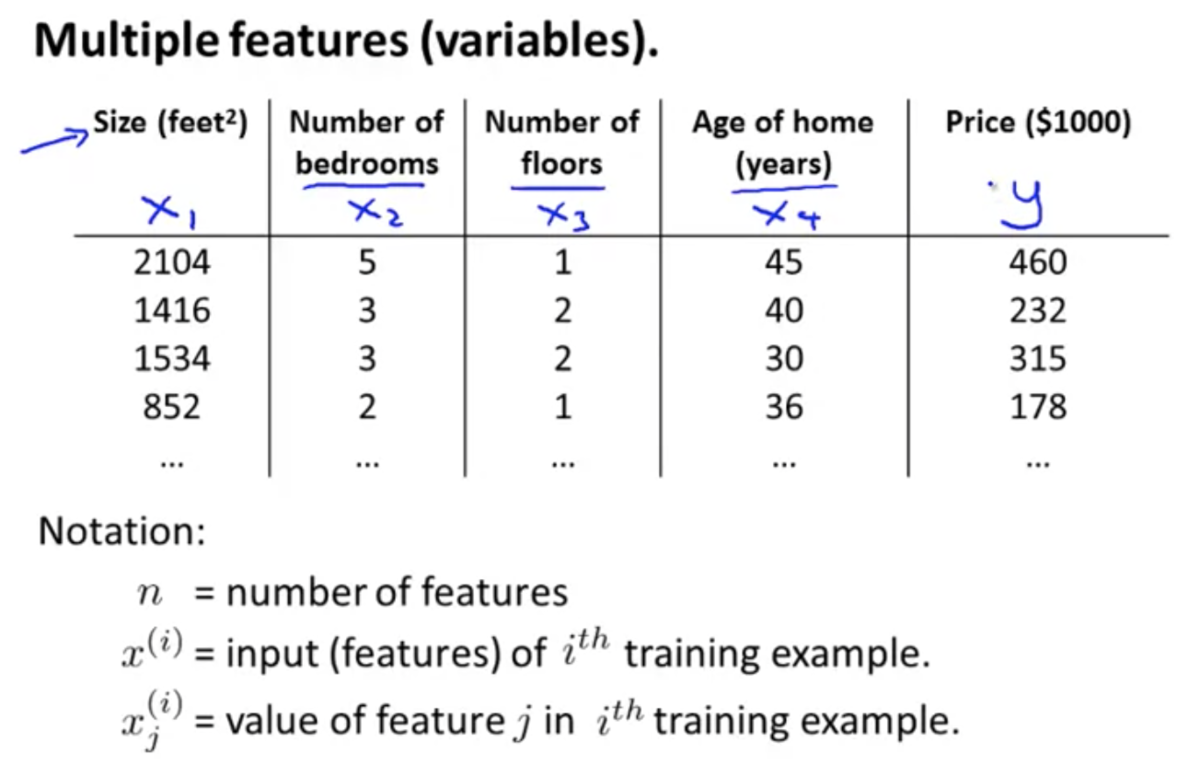
シンボル定義:
のときの仮説関数
:
とおくと、
とかける
→,
はそれぞれn+1次元ベクトルなので、
のようにベクトルの内積としてもかける
このように特徴量が複数ある線形回帰を、多変量線形回帰とも呼ぶ
複数の変数の勾配降下
複数の特徴量を持つ仮説関数に対してどのようにパラメータをフィットさせるか?
勾配降下法を多変量線形回帰に適用する場合を考える
仮説関数、パラメータ、目的関数について:
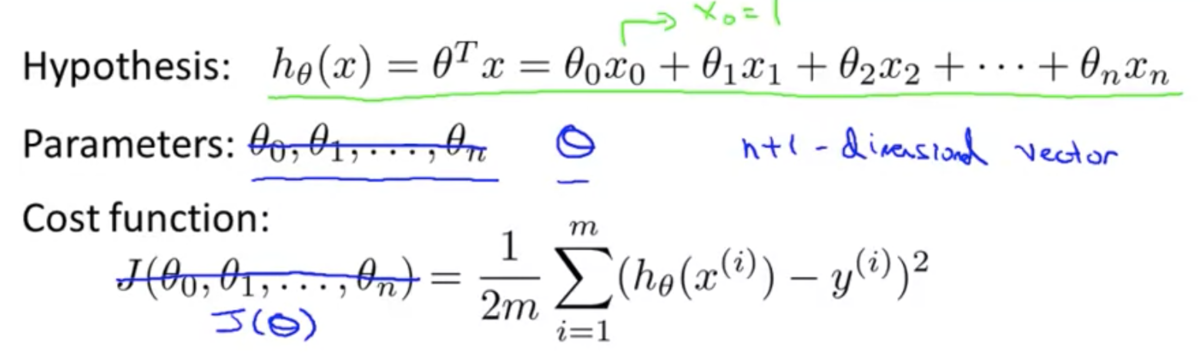
- パラメータ
はn+1次元ベクトルとして考える
はベクトル
を引数にとる関数として考える
勾配降下法は以下のように一般化される

実践における勾配降下法1 - 特徴量スケーリング
勾配降下法は各特徴量のスケールが似ていると早く収束する
事前に各特徴量に正規化を施してスケールを合わせておくことで、収束までの時間を短縮できる
多くの場合、特徴量が の範囲をとるように正規化する
平均ノーマライゼーション (Mean normalization)
正規化の方法のひとつ
i 番目の特徴量 に対して以下の計算をする (ただし
には適用しない)
: 特徴量
の平均値
: 特徴量
の最大値 - 最小値
実践における勾配降下法2 - 学習率
勾配降下法が正しく機能しているか確認する方法
横軸に勾配降下法のイテレーション回数、縦軸に目的関数の値をとって、
の値の推移をプロットする
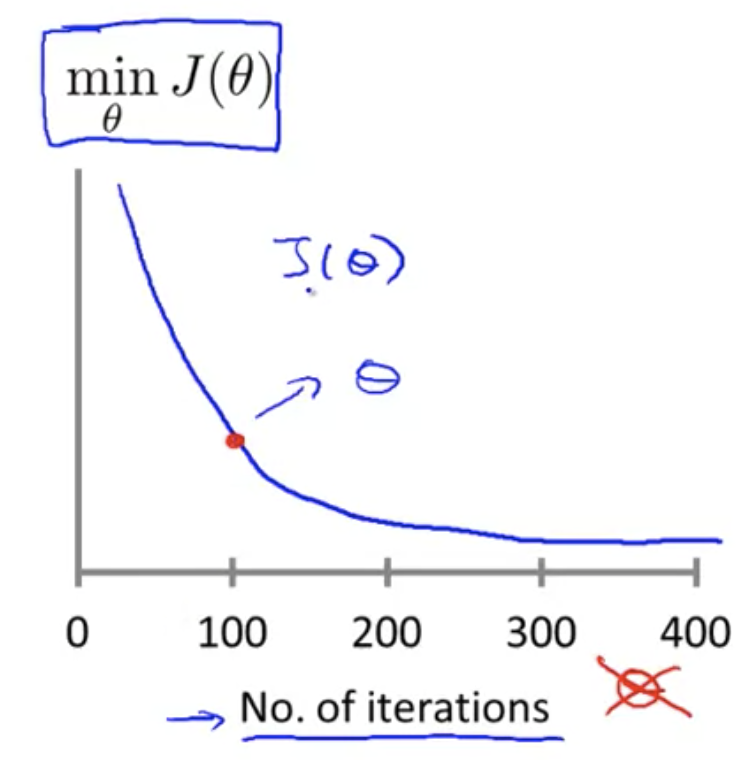
勾配降下法がちゃんと機能していれば、
の値は減少していく
必要なイテレーション回数を事前に知ることは難しい
そのためこのようにプロットして確認することが必要変化率が小さくなってきたらもう収束しているということ
例えば、一回のイテレーションで
が
しか減少しなかったら収束とみなすことで、自動収束テストも可能 (ただしこの閾値を決めるのもまた難しい)
もし
が増加しているようだったら、オーバーシュートを起こしているのかもしれない
その場合は、学習率を小さくすることで改善できる
(もちろんコーディングミスも疑うべき)- また、
が増減を繰り返すような場合もある
その場合も学習率を小さくすることで改善できる
学習率の選び方
ある程度スケールの異なるいくつかの学習率 で
のプロットを行い、
が順調に減少していそうな学習率を選ぶ
これを何度か繰り返す
特徴量と多項式回帰 (Features and Polynomial Regression)
特徴量の選び方について
例えば住宅価格を予測するために『間口の広さ』と『奥行き』という2つの特徴量を持っているとする
この場合、この2つの特徴量をそのまま使うのではなく、2つの掛け合わせて『敷地面積』というひとつの特徴量を作り出してもいい
多項式回帰について
たとえば以下の図のようなデータは、線形回帰だとうまくフィットしなさそうに見える
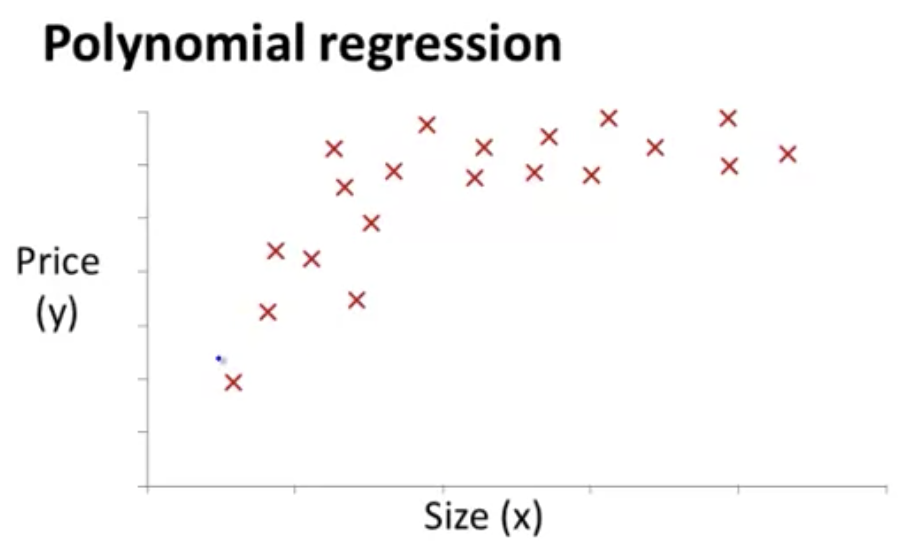
このような場合、例えば のような二次関数を仮説として使うことができる
ただし、二次関数はいずれ弧を描いて下降するため、住宅価格の予測には適さないかもしれない
代わりに のような関数を選べば降下しなくなる
データのフィッティングの仕方はこれまでと変わらず、
の,
,
をそれぞれ
とおけば、これまで見てきたような
という式として考えることができる
住居の価格としてフィッティングしそうな関数を挙げるとすれば以下のようなもの
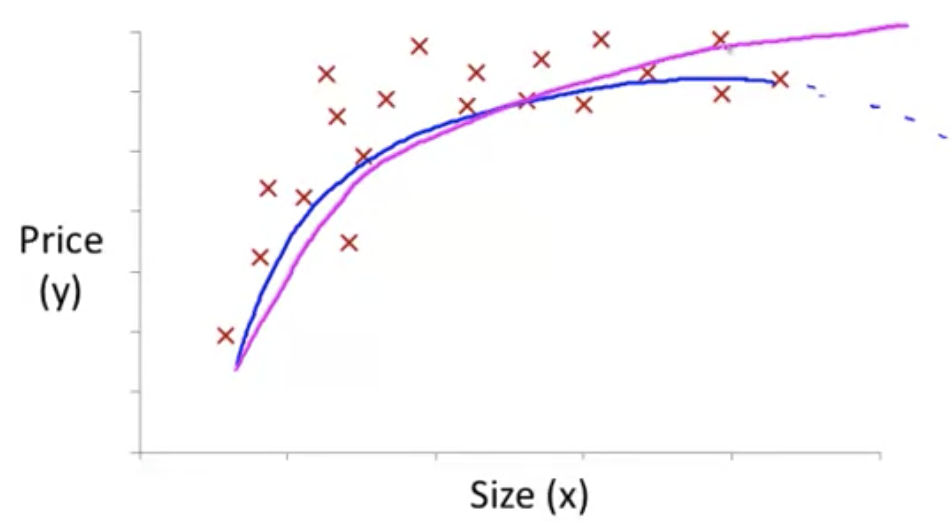
パラメータの解析的計算 (Computing Parameters Analytically)
正規方程式 (Normal Equation)
目的関数を最小化する方法として、勾配降下法の他に、正規方程式を解くという方法がある
正規方程式を使ってパラメータを解析的に解くと、一度に全てのパラメータを求めることができる
目的関数を最小化するには
(for every
)
を解けばいい
すると
を得る これが正規方程式
(は逆行列)
XとYの例
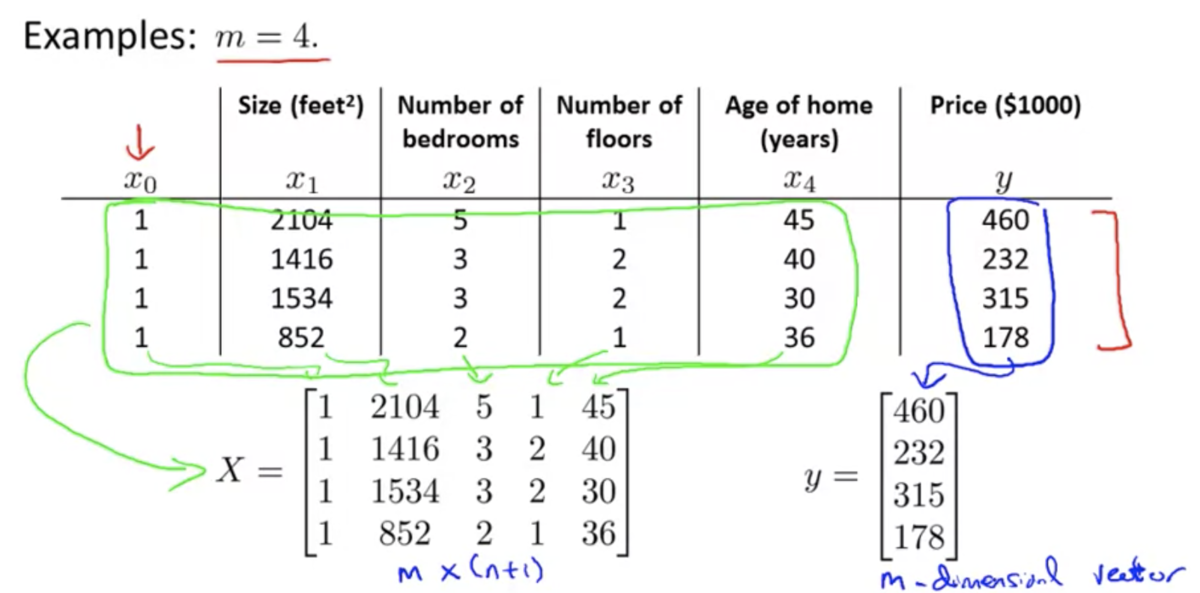
正規方程式を使う場合、特徴量スケーリングは必要ない
正規方程式は、線形回帰では使えるが、より複雑な学習アルゴリズム(ロジスティック回帰など)ではうまく機能しない
勾配降下法と正規方程式のメリット・デメリット
勾配降下法
- メリット
- 特徴量の種類の数が多くても機能する
- デメリット
- 適切な学習率
を試行錯誤して見つける必要がある
- 多くのイテレーションが必要
- 適切な学習率
正規方程式
- メリット
- 学習率
を必要としない
- イテレーションを回す必要がない
- 学習率
- デメリット
- 特徴量の種類の数が多いと計算コストが跳ね上がる
- 逆行列計算の計算オーダーは
らしい
- 経験則として、n = 100 ~ 1000程度なら全然大丈夫、n = 10000くらいになると悩み始めるとのこと
- 逆行列計算の計算オーダーは
- 特徴量の種類の数が多いと計算コストが跳ね上がる
正規方程式の非可逆性 (Normal Equation Noninvertibillity)
補足的な内容らしいのでとばした
第1週:導入【Coursera Machine Learningコース】
Introduction
機械学習とは?
アーサーサミュエルの定義:コンピュータに明示的にプログラムすることなく学習する能力を与える研究分野
教師あり学習 (Supervised Learning)
- 教師あり学習では、全てのサンプルについて「正しい答え」が与えられている
- 予測したい値が連続値なら回帰問題
- 予測したい値が離散値なら分類問題
教師なし学習 (Unsupervised Learning)
データセットから構造を見つける
Model and Cost Function
モデル表現 (Model Representation)
線形回帰
- 例:住宅価格と敷地面積から線形関係を見つける
シンボル定義:
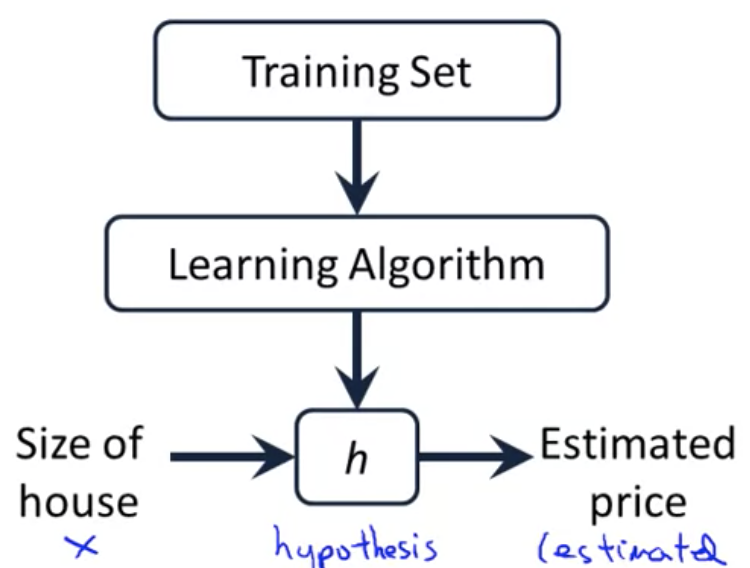
教師あり学習の仕組み
仮説関数をどう表すか
- 単回帰 ... 変数が1つの線形モデル
目的関数 (Cost Function)
- データに対しどのように最適な直線(線形回帰の場合)を当てはめるか算出するために役立つ
仮説関数の
はパラメータと呼ぶ
- 例 :
における
,
- 例 :
パラメータの値によって異なった仮説になる
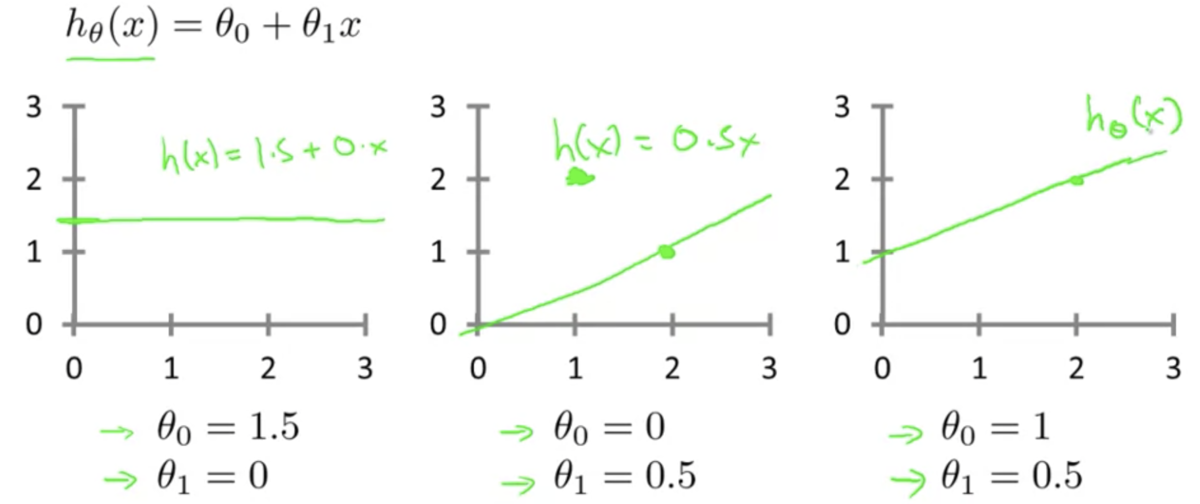
どうすれば最適な
,
が得られる? → 目的関数
を最小化する

目的関数の直感的理解 1 (Cost Function - Intuition 1)
(とするとき)
とデータセットのズレが大きいほど誤差が指数的に大きくなる
⇆ 仮説関数がデータに最もフィットするとき誤差が最も小さくなる
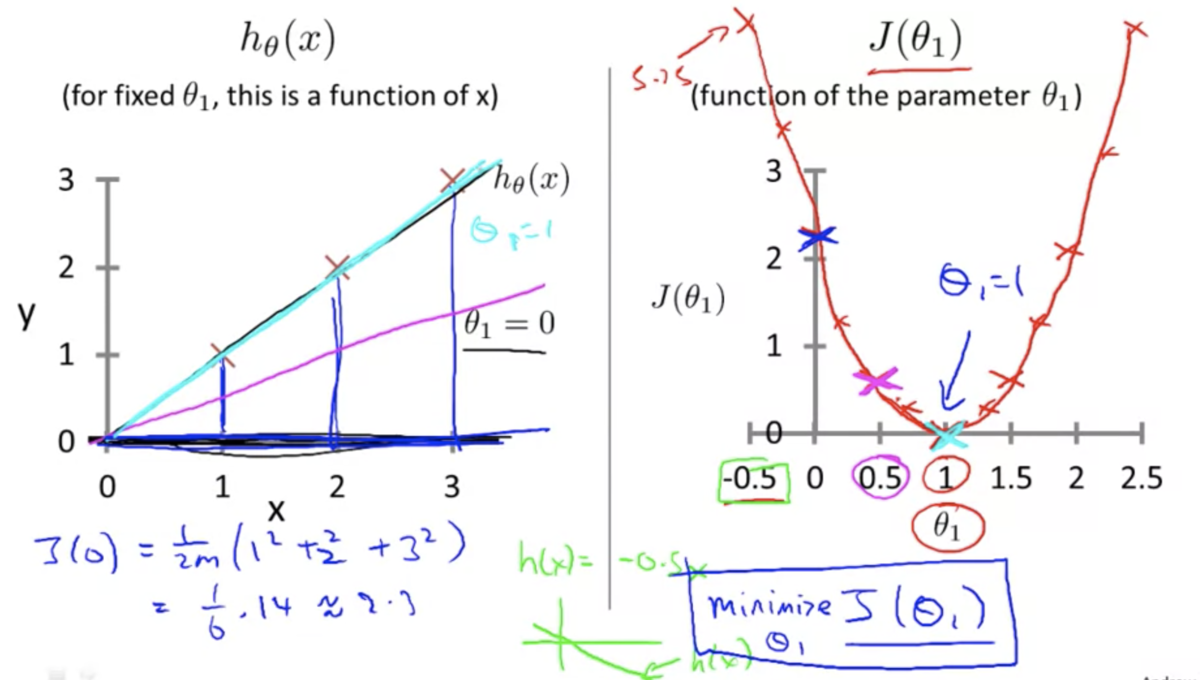
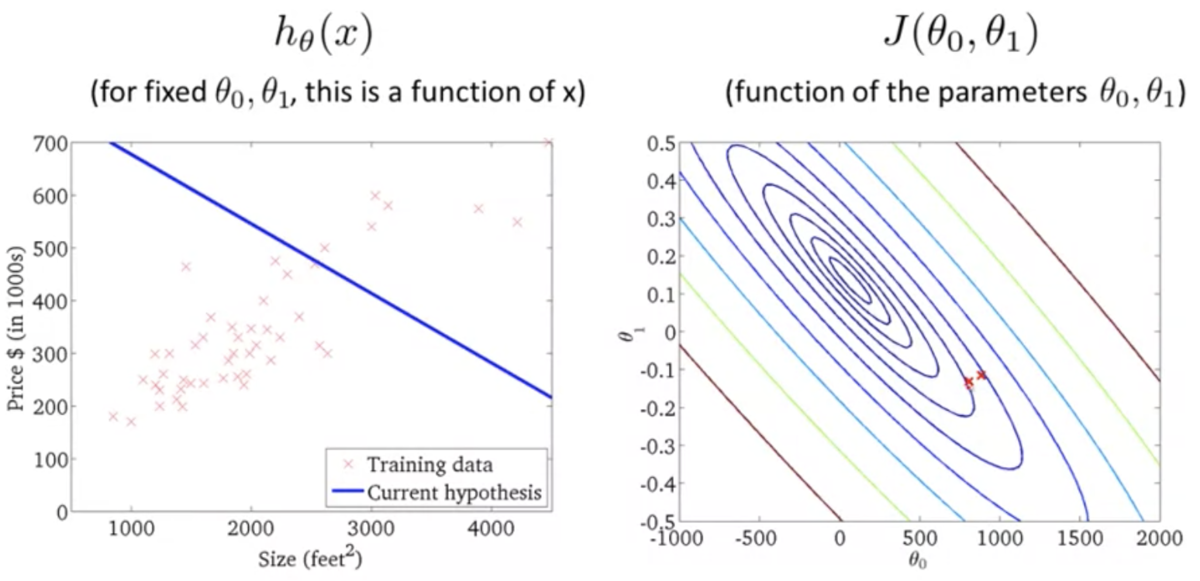
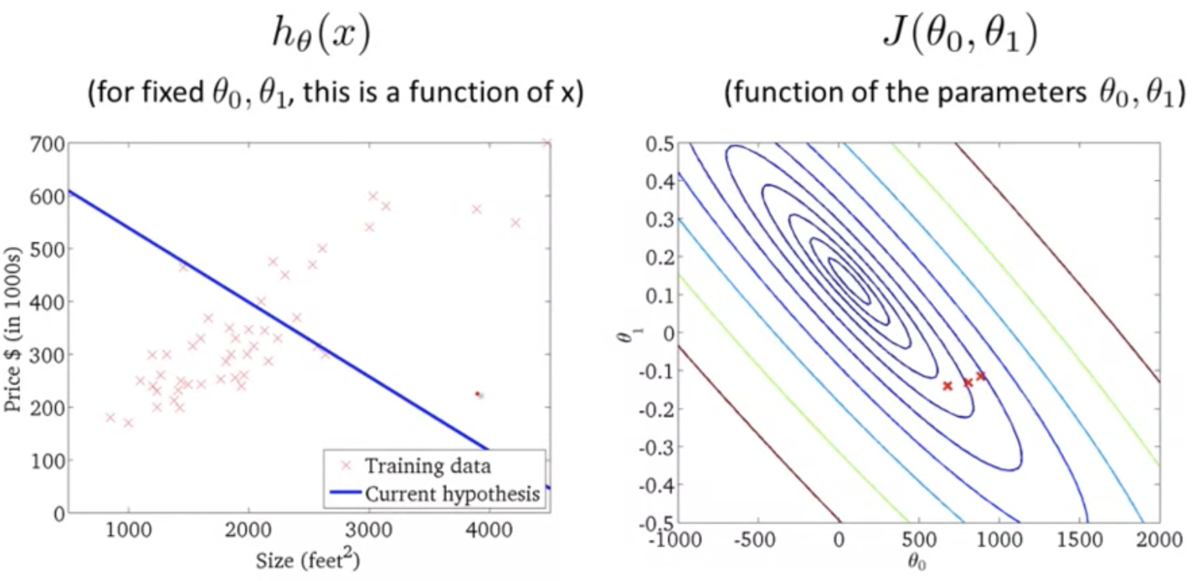
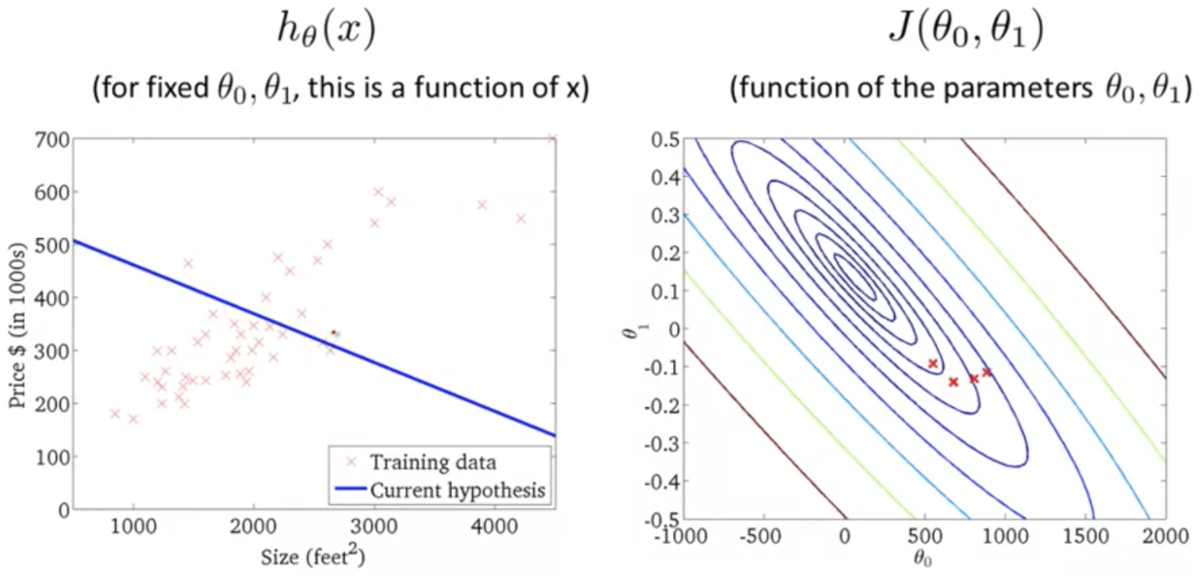
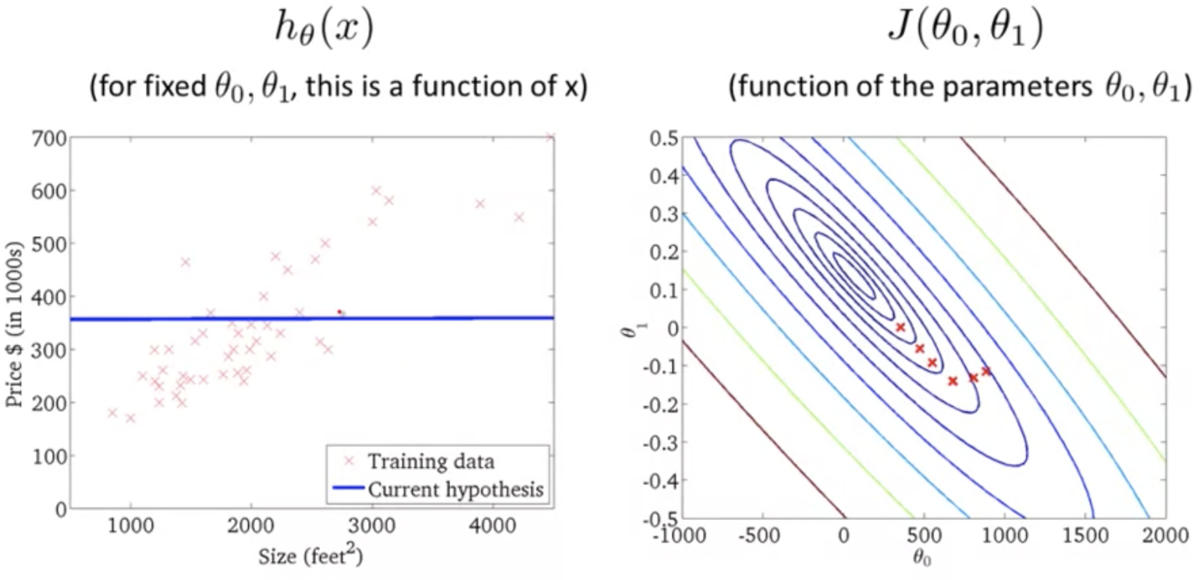
目的関数の直感的理解 2 (Cost Function - Intuition 2)
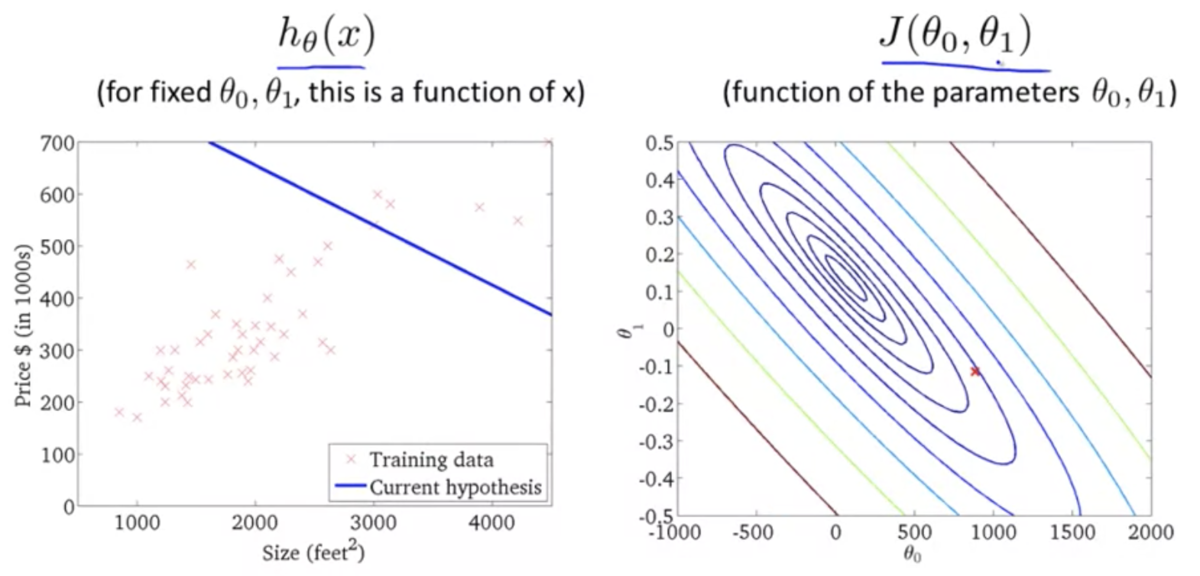
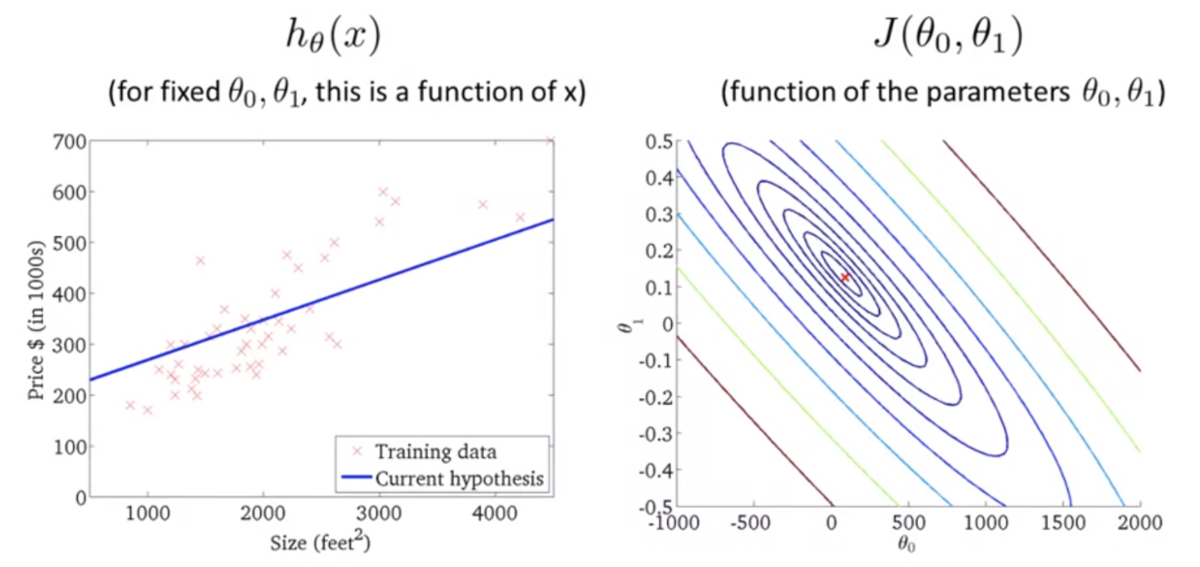
- 仮説関数が単回帰モデルのときの目的関数のプロット (3次元)
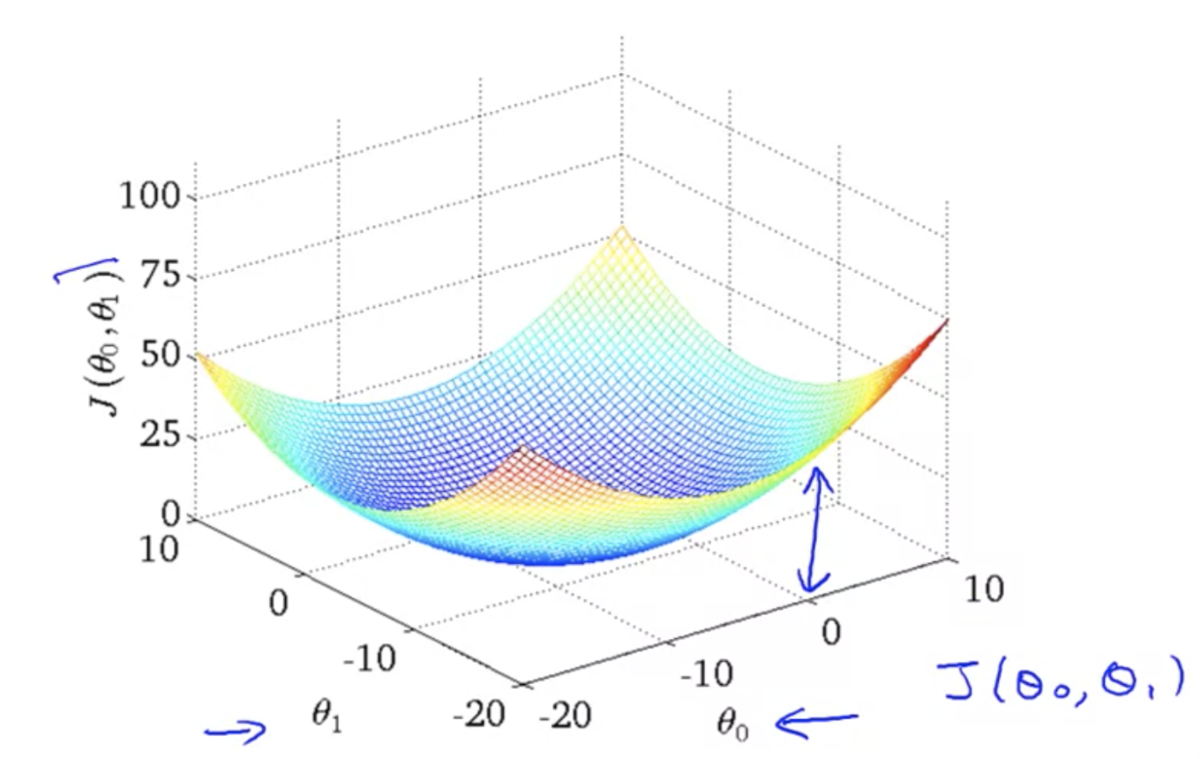
上記の2次元バージョン (等高線)
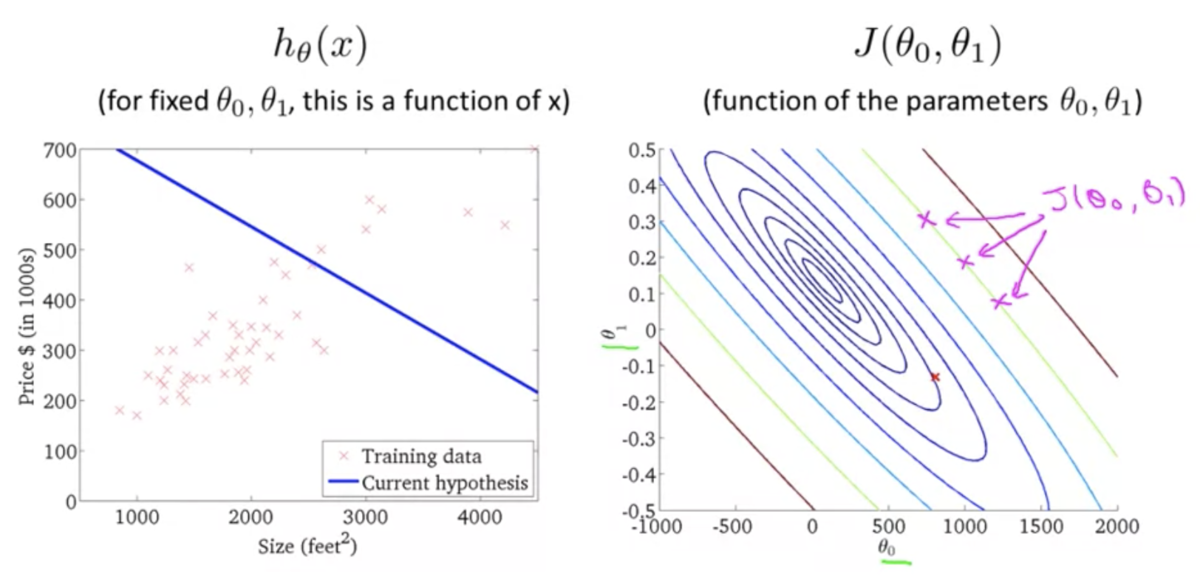
仮説関数がデータにフィットするほど誤差が小さくなるのがわかる
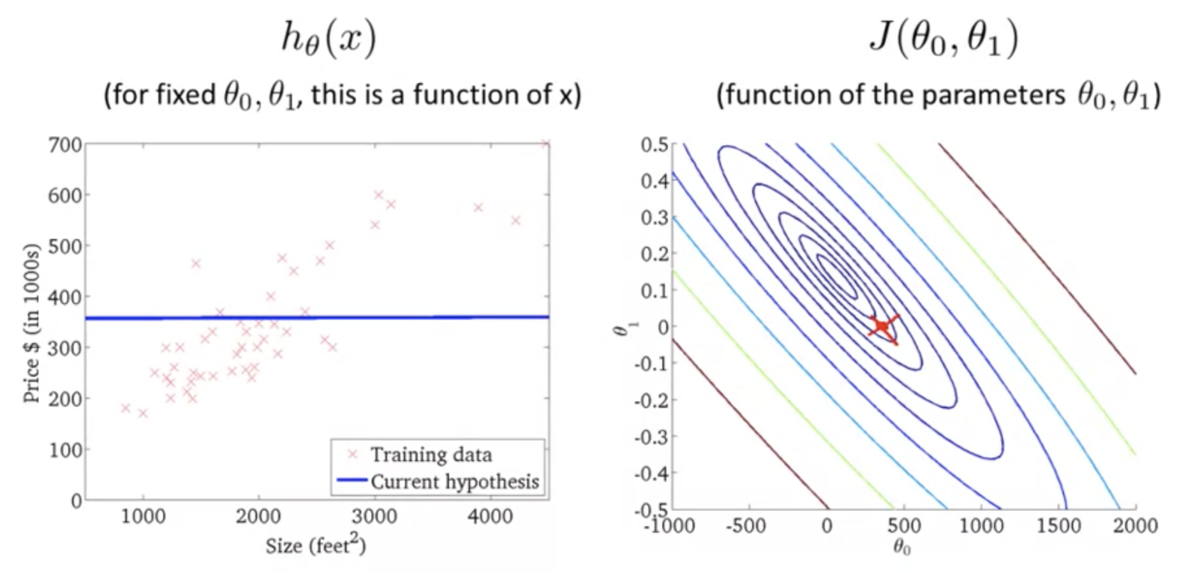
パラメータ学習 (Parameter Learning)
勾配降下法 (Gradient Descent)
目的関数
を最小化するアルゴリズムのひとつ
線形回帰以外でも使われる汎用的なアルゴリズム
例:
,
をパラメータにもつ目的関数
を最小化する
勾配降下法の基本的な考え方:
,
になんらかの初期値を与える
- 初期値はなんでもよいが、0初期化が一般的
,
の値を少しづつ変化させて
が減少するか試す
が減少する方向に
,
を変化させることを繰り返すと、いずれは最小値、あるいは局所的最小値に辿り着く
三次元的なイメージ
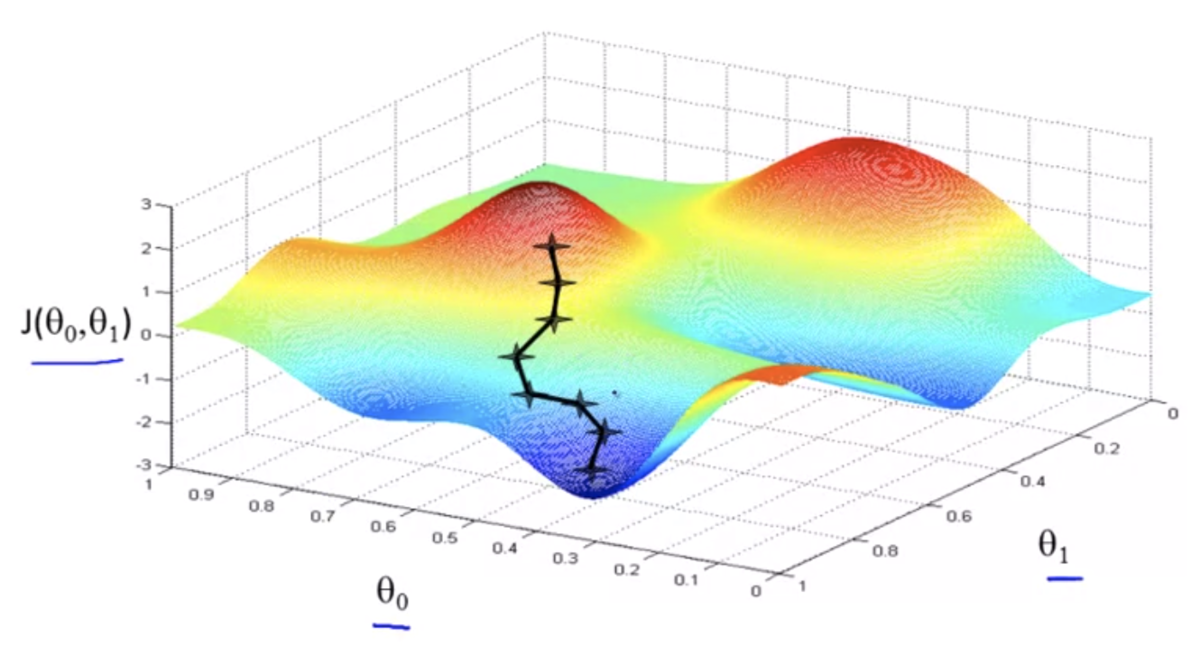
初期値が異なると、異なる解にたどり着くこともある
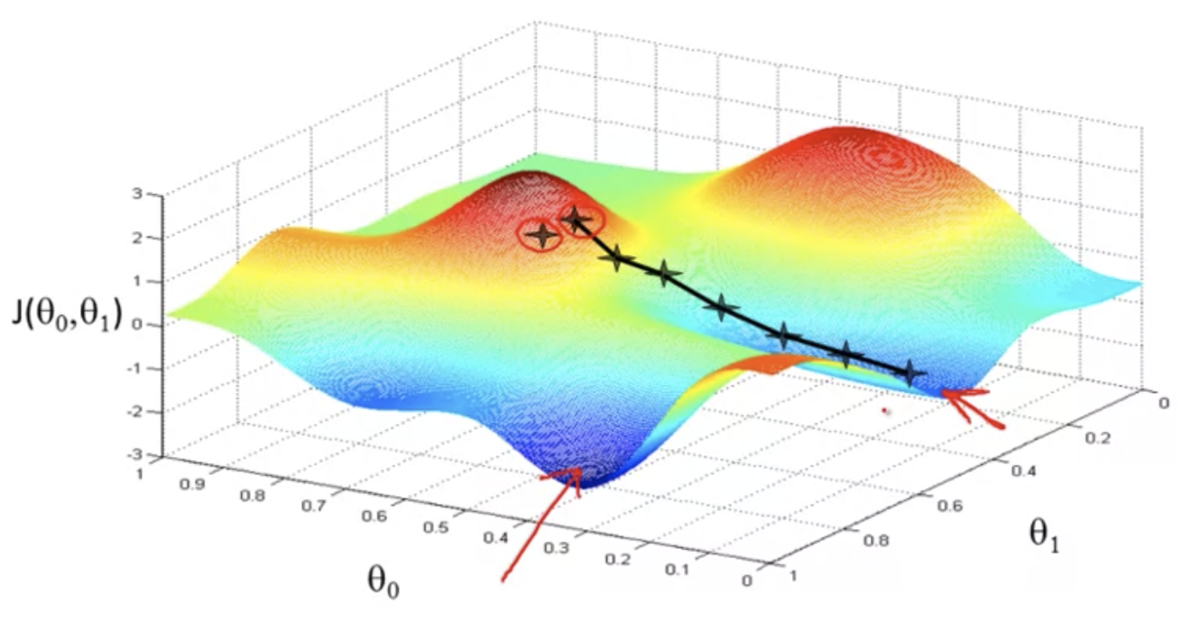
数学的表現:

- "
"は
を
に代入することを意味する
: 学習率 (
)
- 降下するステップの大きさを決める
: 導関数項 (解説は先の章)
,
は同時に更新するように実装すること
- 一方を更新した後、更新した値を使って他方を計算しないように
- "

勾配降下法の直感的理解 (Gradient Descent Intuition)
目的関数のパラメータが
のみの場合の勾配降下法を考える
は実数 (
R)
導関数項について:
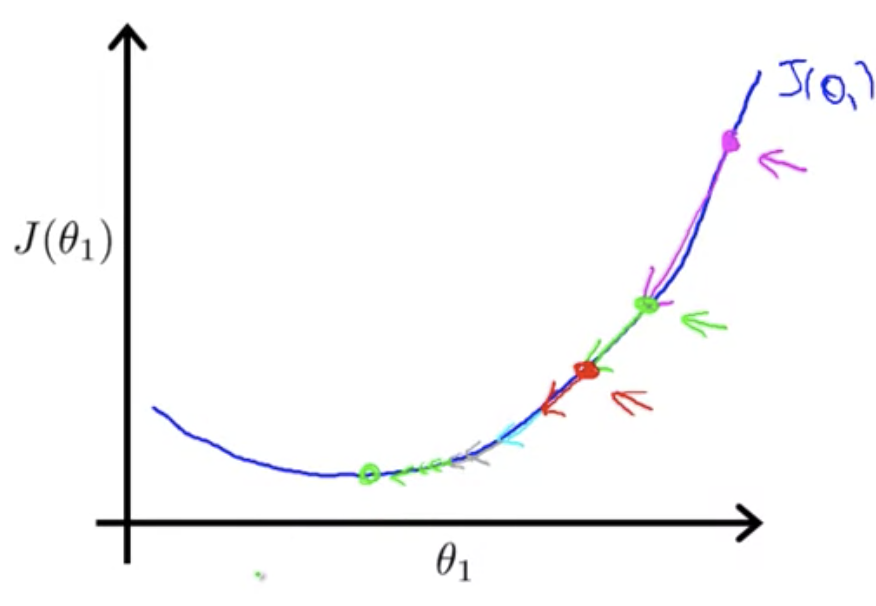
微分とは接線の傾きを調べること
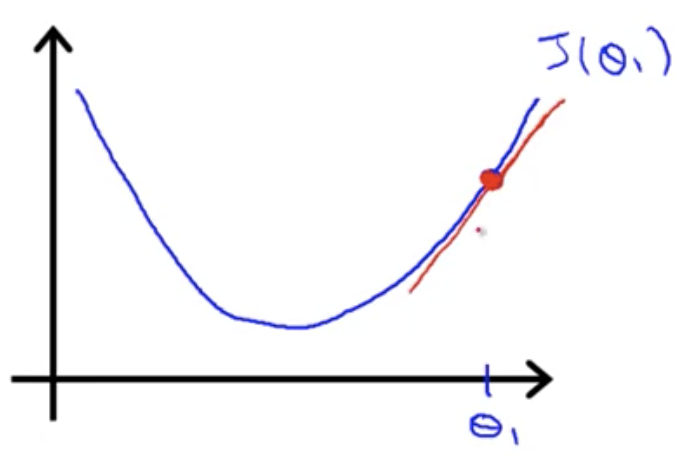
傾きが正か負かによって
の更新方向が決まる
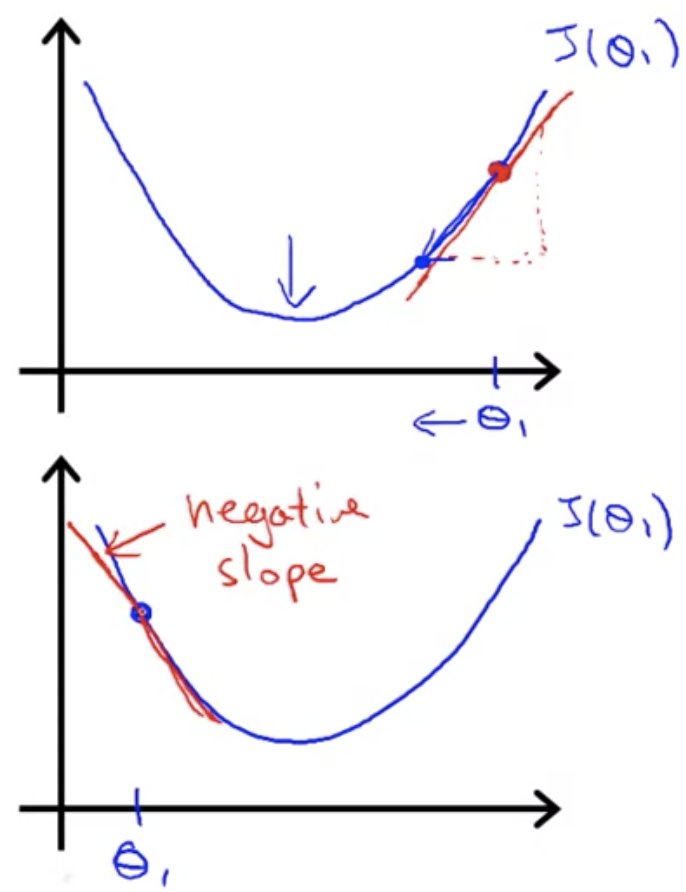
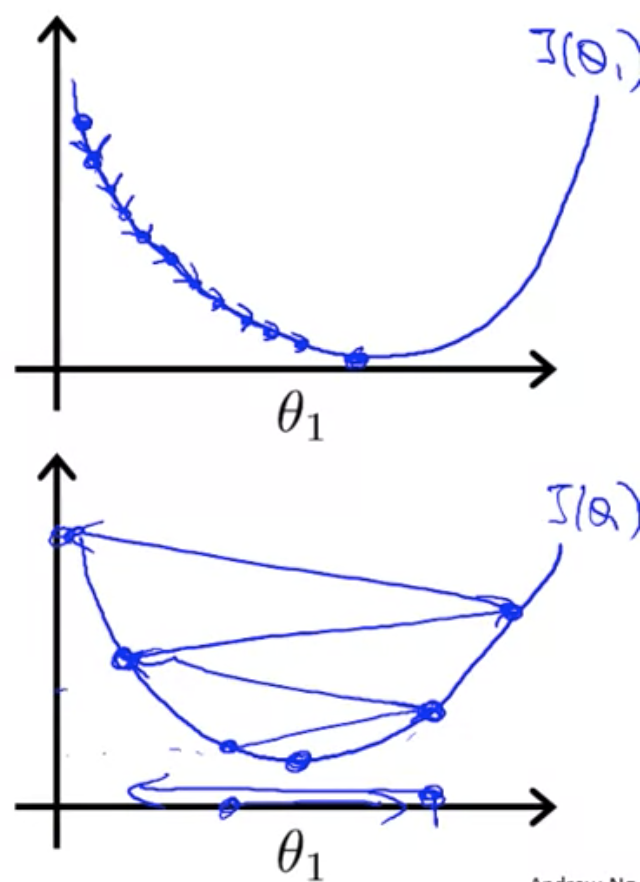
学習率
が小さすぎると収束まで時間がかかり、大きすぎると収束しなかったり発散してしまったりする
が局所的最適解で初期化されると、傾きが0になり更新されない
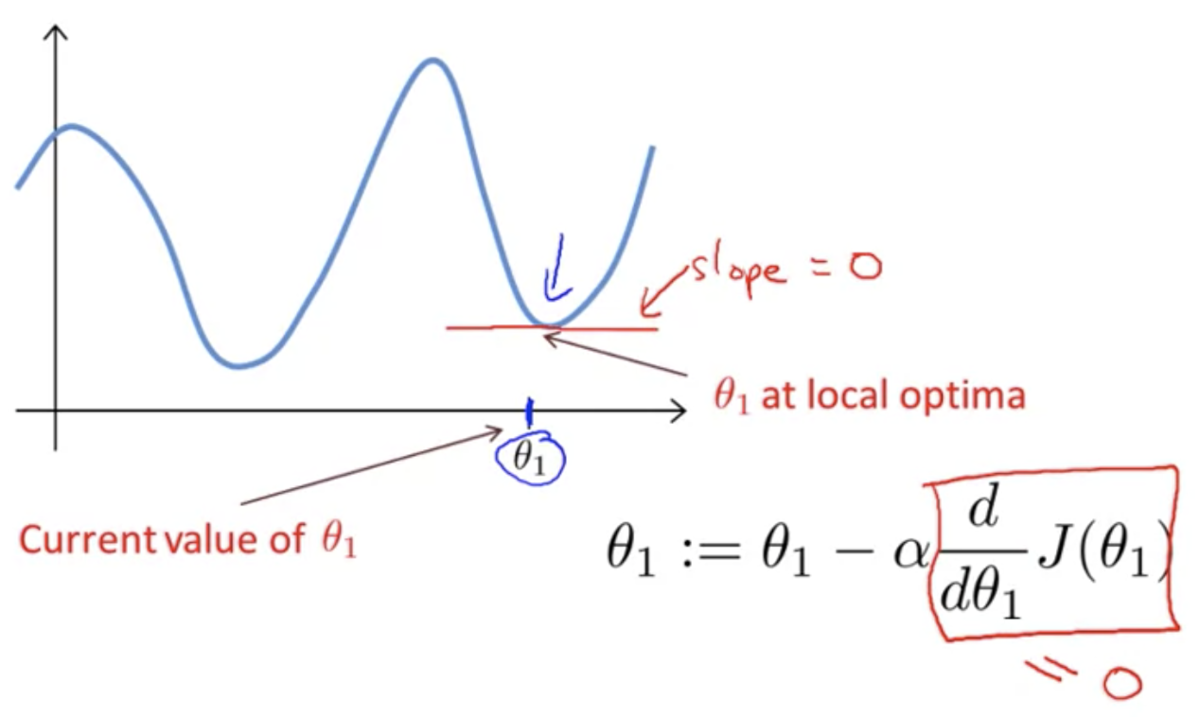
を適切な学習率で更新するたびに、傾きは小さくなり(最急降下法のステップが小さくなり)、最終的に(局所的)最小値に収束する