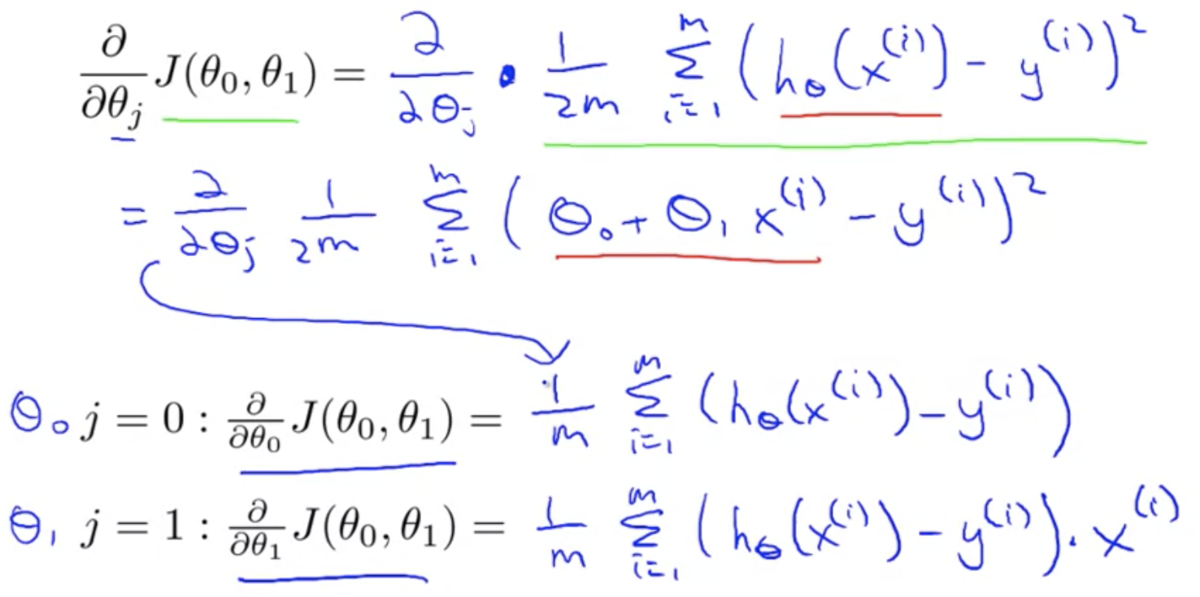第1週：導入【Coursera Machine Learningコース】

Introduction

機械学習とは？

アーサーサミュエルの定義：コンピュータに明示的にプログラムすることなく学習する能力を与える研究分野

教師あり学習 (Supervised Learning)

教師あり学習では、全てのサンプルについて「正しい答え」が与えられている
予測したい値が連続値なら回帰問題
予測したい値が離散値なら分類問題

教師なし学習 (Unsupervised Learning)

データセットから構造を見つける

Model and Cost Function

モデル表現 (Model Representation)

線形回帰
- 例：住宅価格と敷地面積から線形関係を見つける
シンボル定義：
- $m$ : トレーニングサンプルの数
- $x$ : 入力変数（特徴量）
- $y$ : 出力変数（目的変数）
- 一件のトレーニングサンプルは $(x, y)$ のように書き表す
- i番目のトレーニングサンプルは $(x^ {(i)}, y^ {(i)})$ のように書き表す
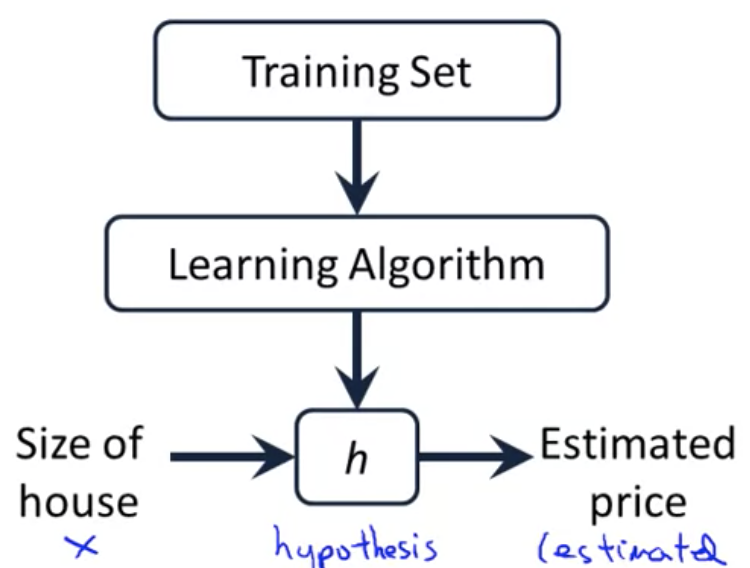
教師あり学習の仕組み
1. トレーニングセットを学習アルゴリズムに与える
2. 学習アルゴリズムはある関数 $h$ を出力する ( $h$ は仮説"hypothesis"の頭文字)
  "仮説"という名前は歴史的経緯で定着した呼び方らしい
3. 関数hに入力を与えると予測値が出力される
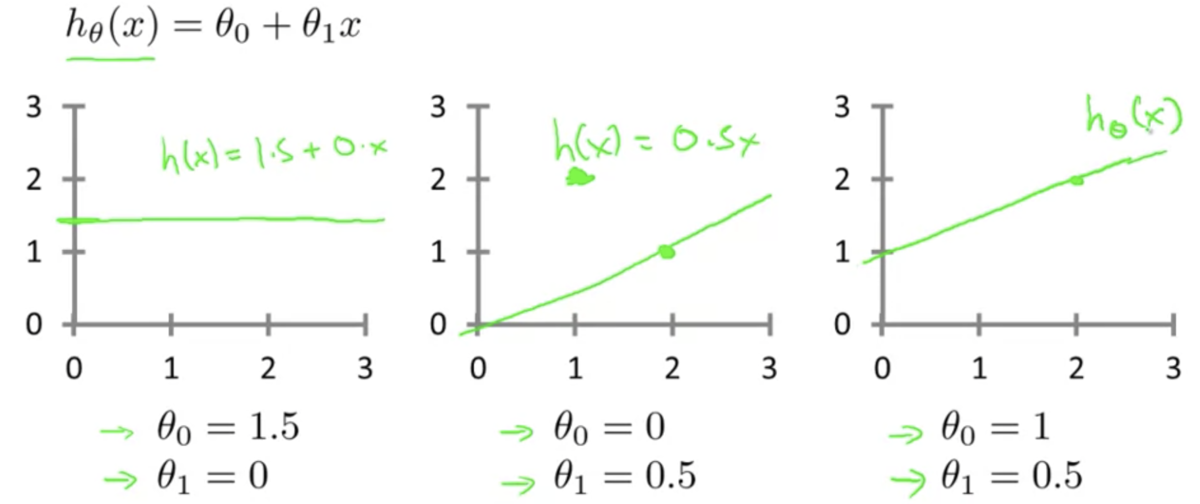
仮説関数をどう表すか
- - 単回帰 ... 変数が1つの線形モデル

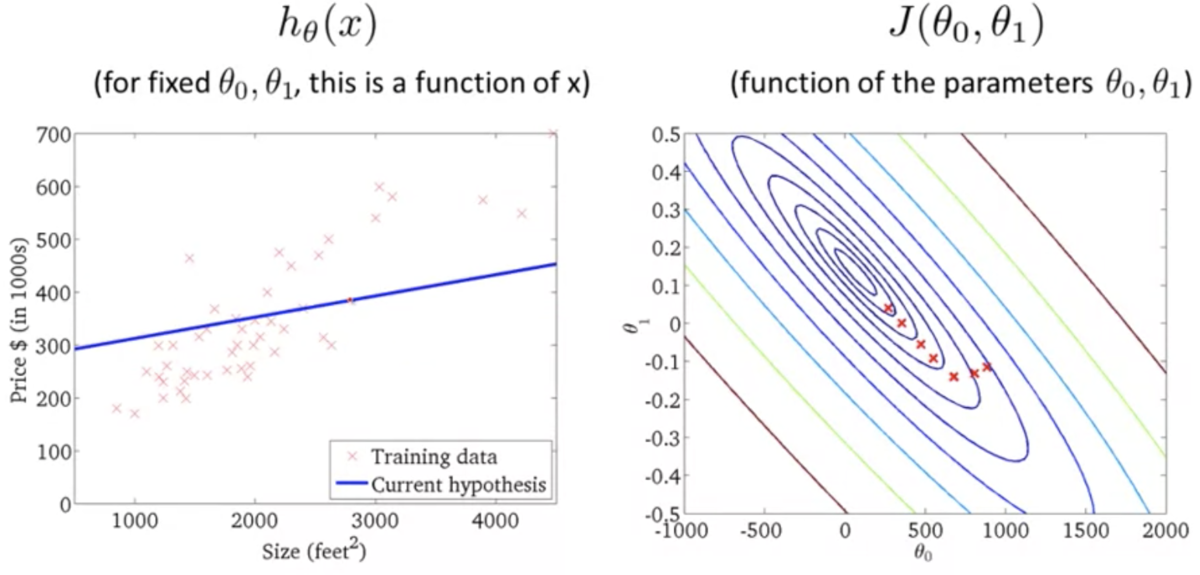
目的関数 (Cost Function)

データに対しどのように最適な直線(線形回帰の場合)を当てはめるか算出するために役立つ
仮説関数の $θ$ はパラメータと呼ぶ
- 例 : $h_θ(x)=θ _ 0+θ _ 1x$ における $θ _ 0$ , $θ _ 1$
パラメータの値によって異なった仮説になる
どうすれば最適な $θ _ 0$ , $θ _ 1$ が得られる？ → 目的関数 $J$ を最小化する

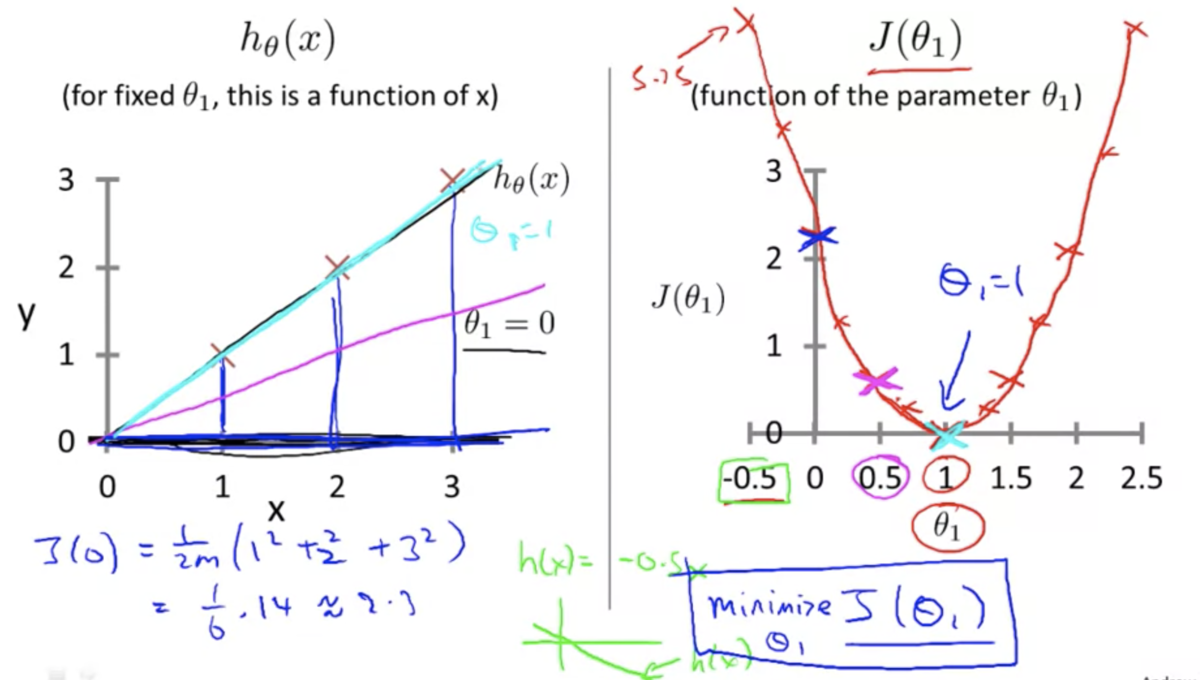
目的関数の直感的理解 1 (Cost Function - Intuition 1)

( $θ _ 0 = 0$ とするとき)
$h_ θ(x)$ とデータセットのズレが大きいほど誤差が指数的に大きくなる
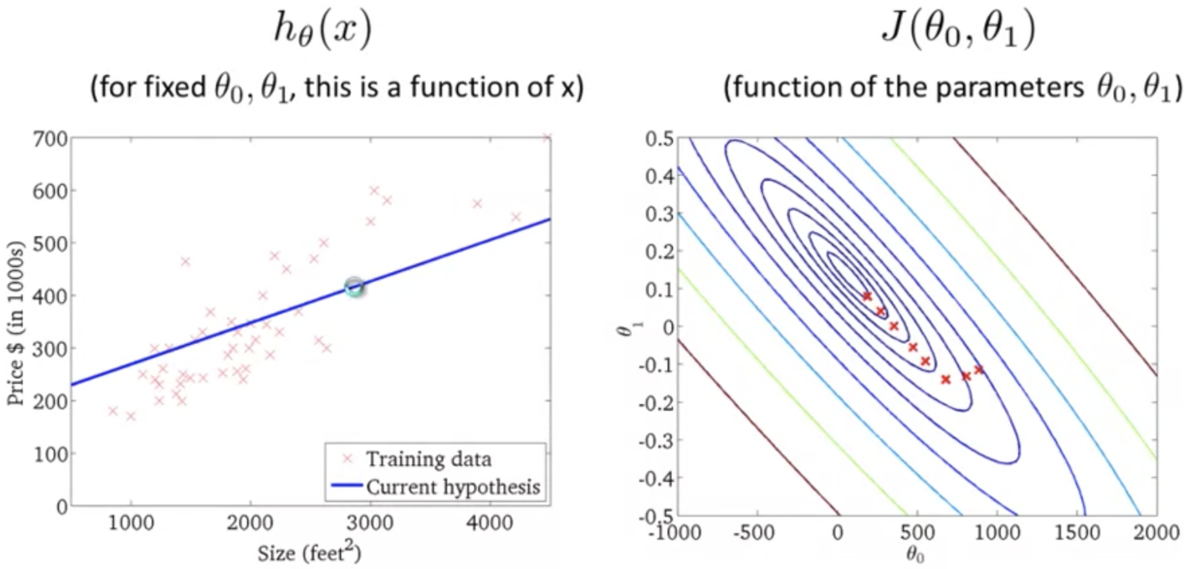
⇆ 仮説関数がデータに最もフィットするとき誤差が最も小さくなる
f:id:sasakino:20200820212252p:plain:w500

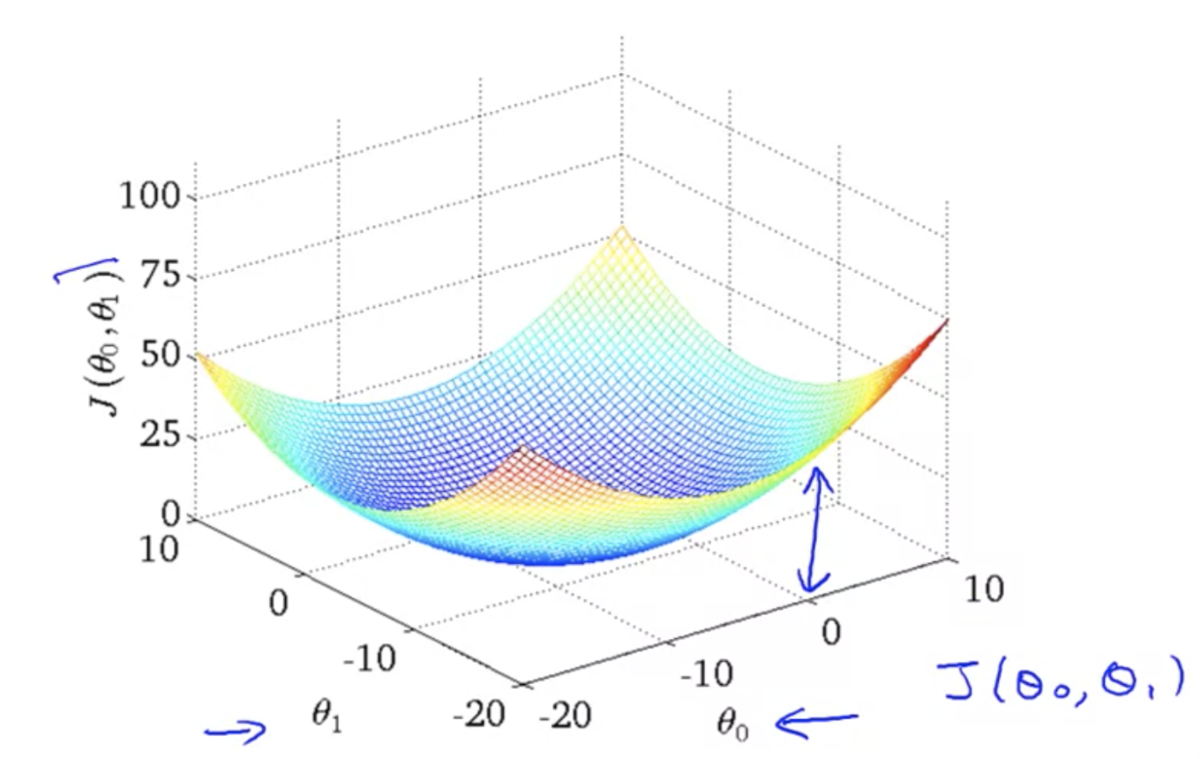
目的関数の直感的理解 2 (Cost Function - Intuition 2)

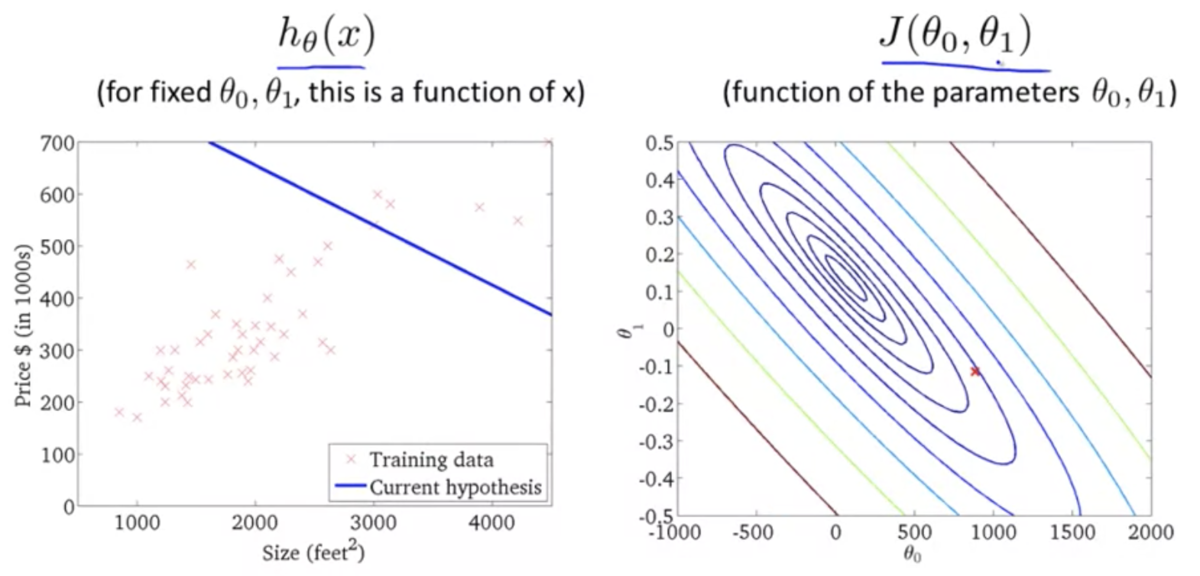
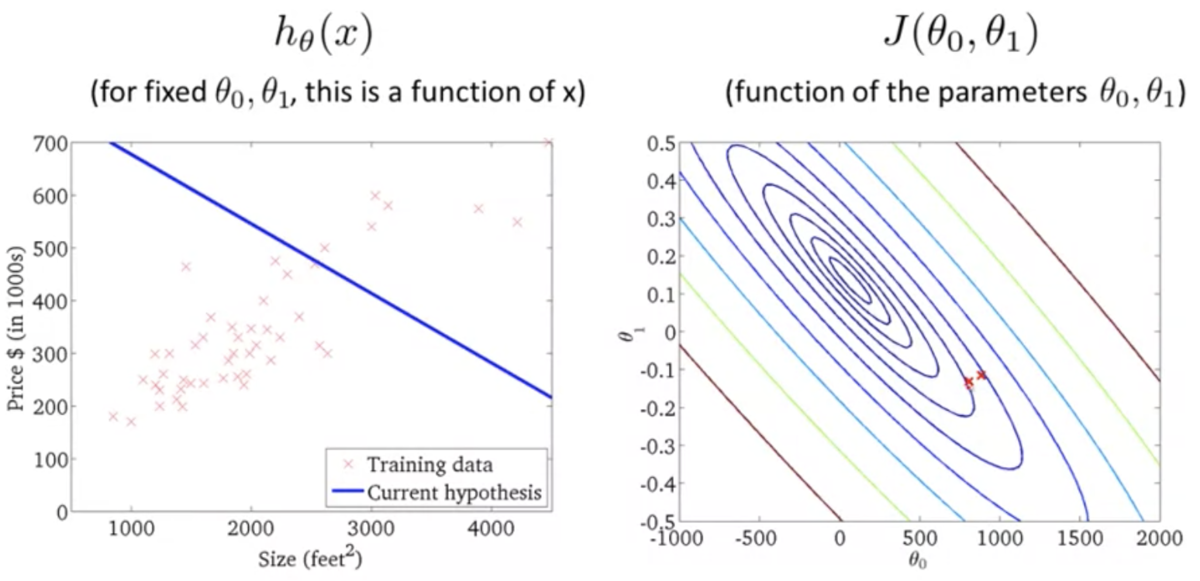
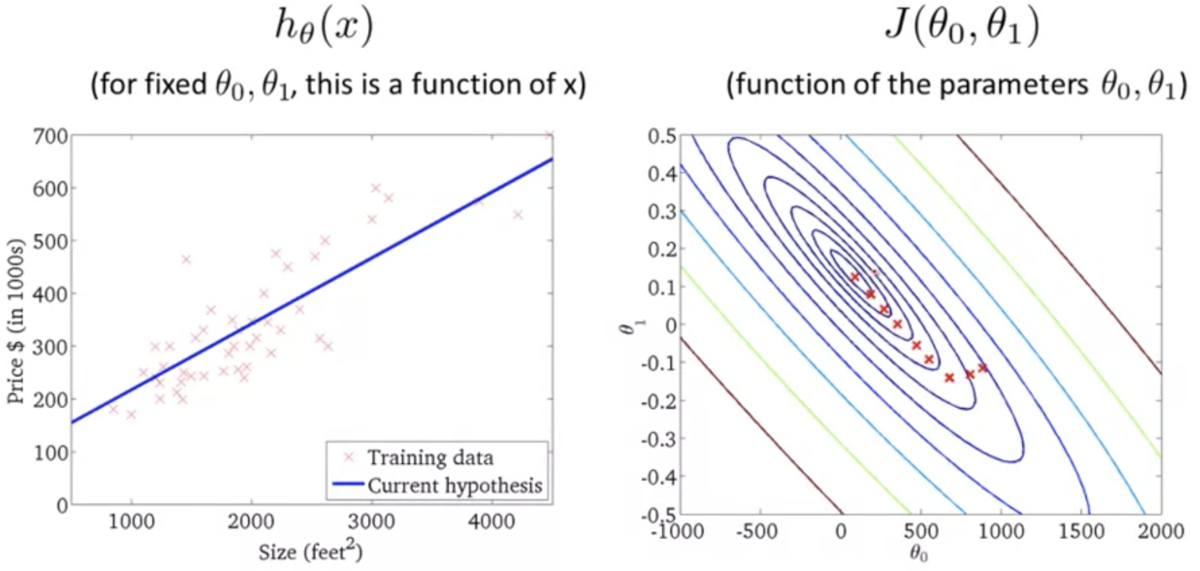
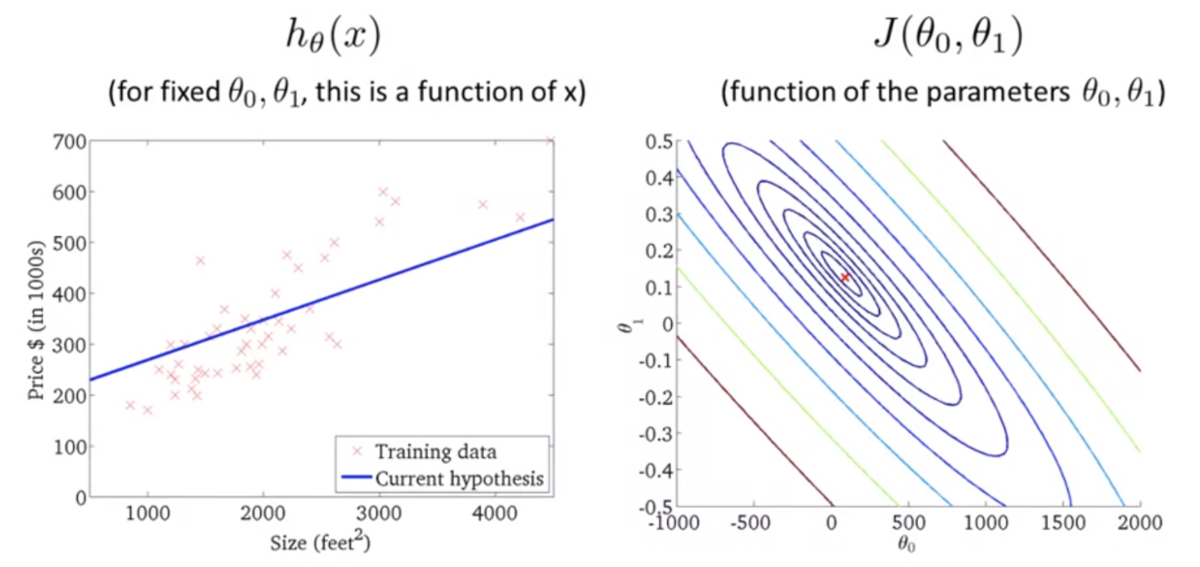
仮説関数が単回帰モデルのときの目的関数のプロット (3次元)

f:id:sasakino:20200820213912p:plain:w400

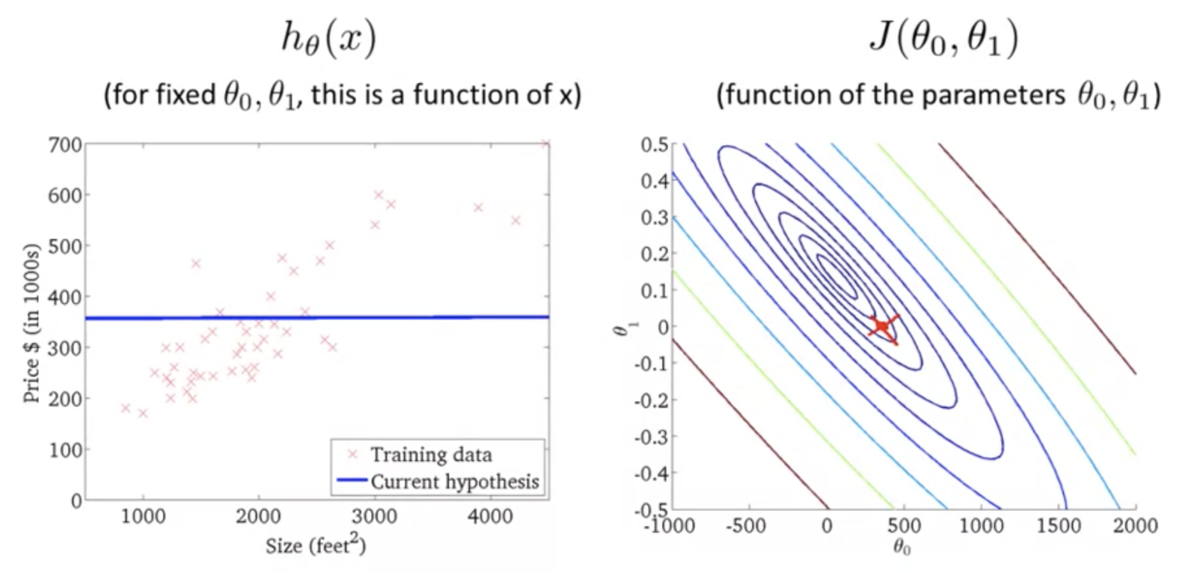
上記の2次元バージョン (等高線)
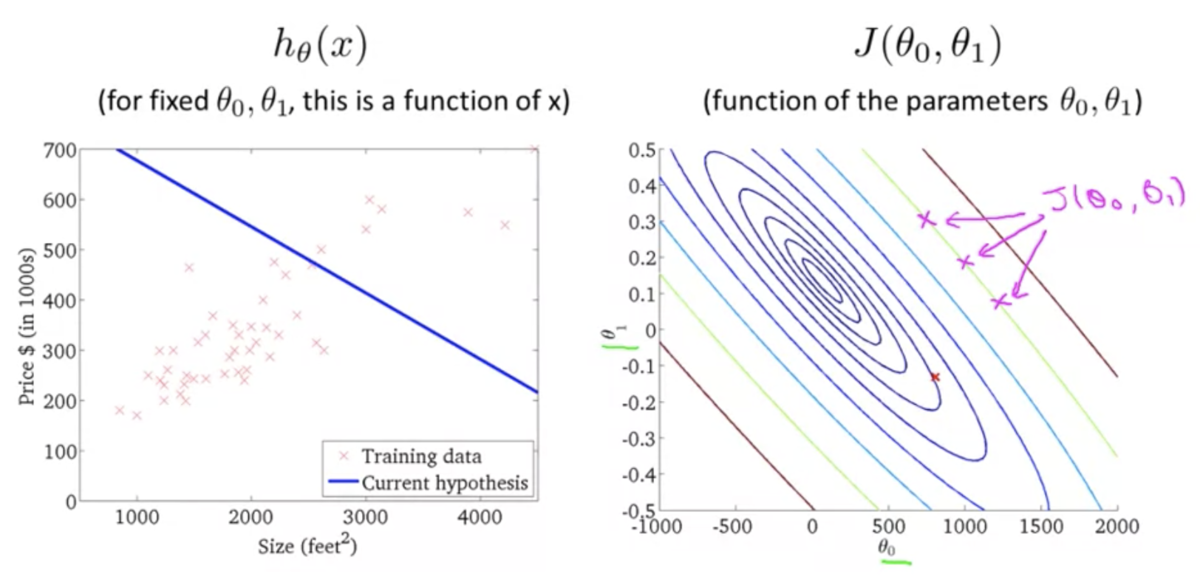
仮説関数がデータにフィットするほど誤差が小さくなるのがわかる

f:id:sasakino:20200820215216p:plain:w500
f:id:sasakino:20200820215242p:plain:w500

パラメータ学習 (Parameter Learning)

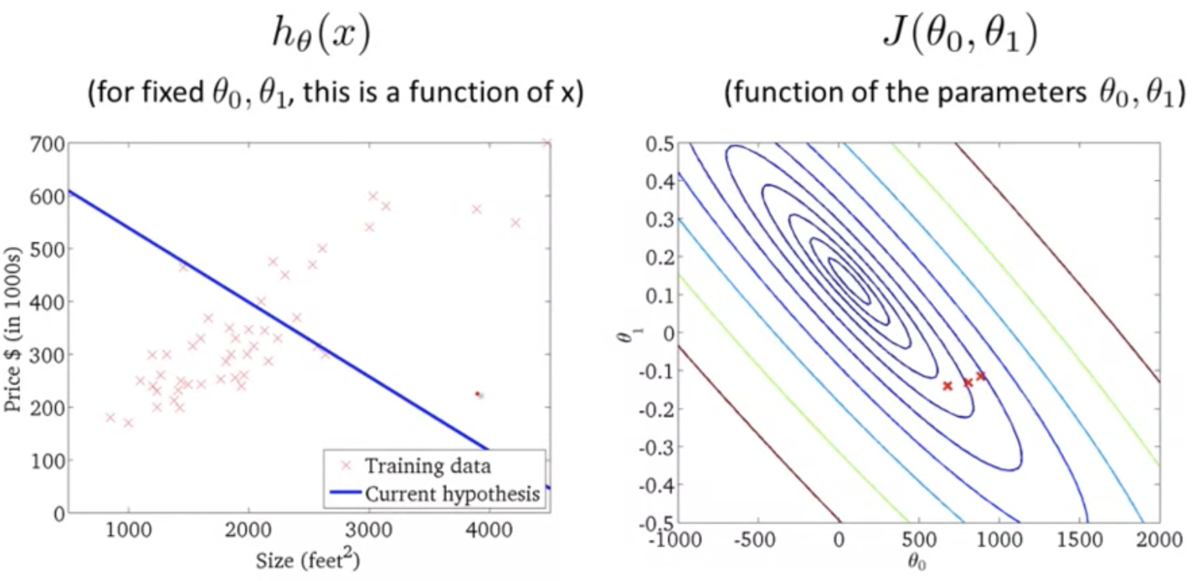
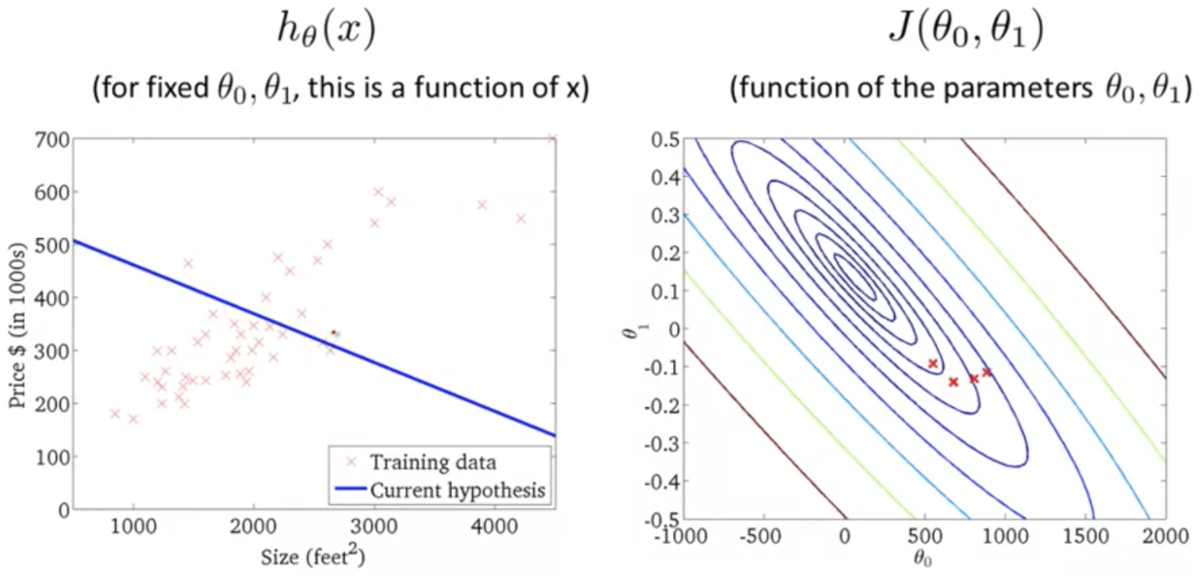
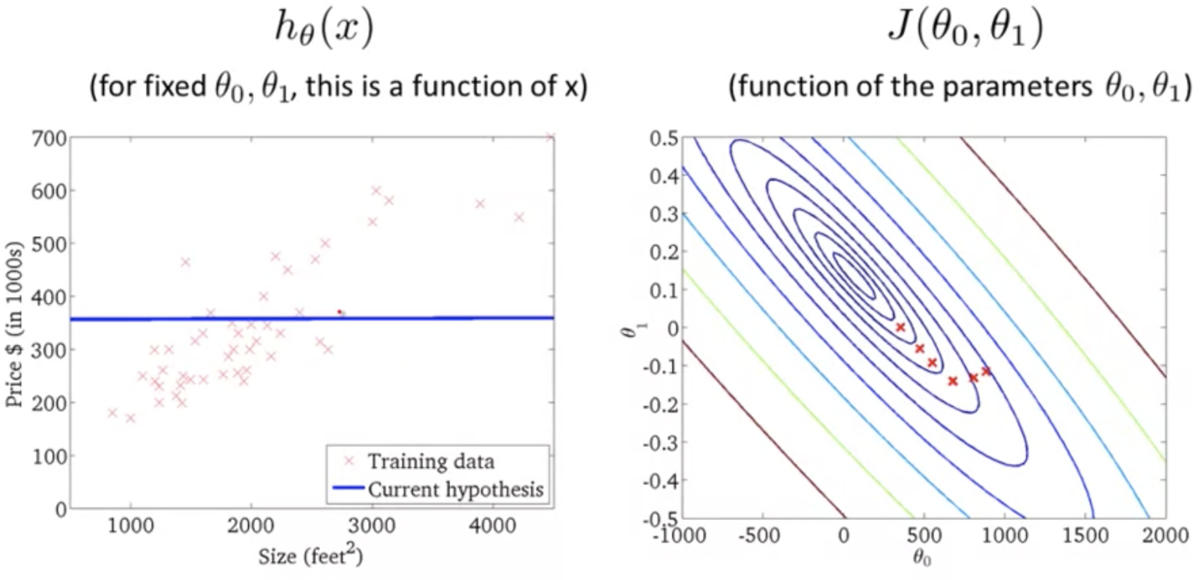
勾配降下法 (Gradient Descent)

目的関数 $J$ を最小化するアルゴリズムのひとつ
線形回帰以外でも使われる汎用的なアルゴリズム
例： $θ _ 0$ , $θ _ 1$ をパラメータにもつ目的関数 $J$ を最小化する
- 勾配降下法の基本的な考え方：
  - , になんらかの初期値を与える
    - 初期値はなんでもよいが、0初期化が一般的
  - $θ _ 0$ , $θ _ 1$ の値を少しづつ変化させて $J$ が減少するか試す
  - $J$ が減少する方向に $θ _ 0$ , $θ _ 1$ を変化させることを繰り返すと、いずれは最小値、あるいは局所的最小値に辿り着く
- 三次元的なイメージ
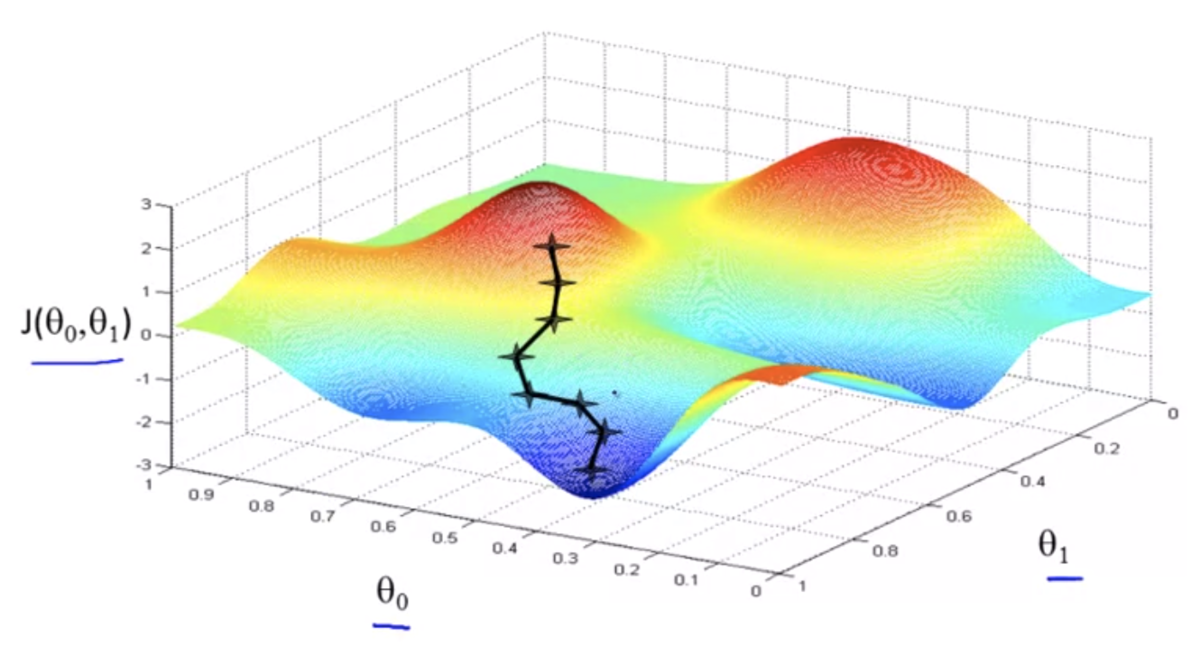
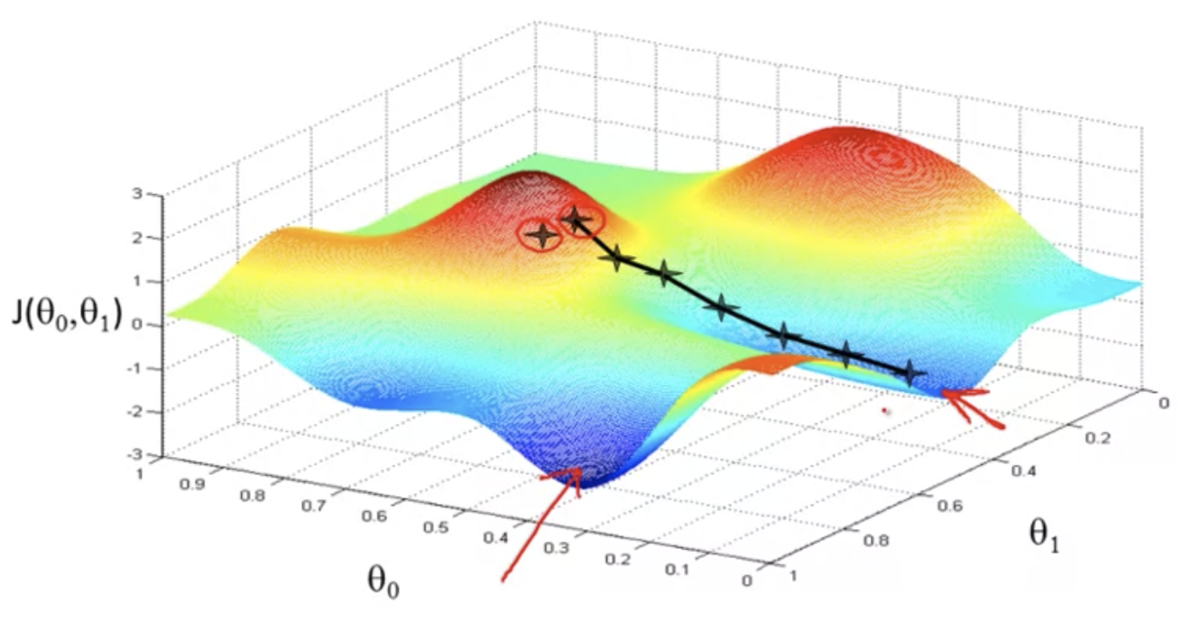
- 初期値が異なると、異なる解にたどり着くこともある
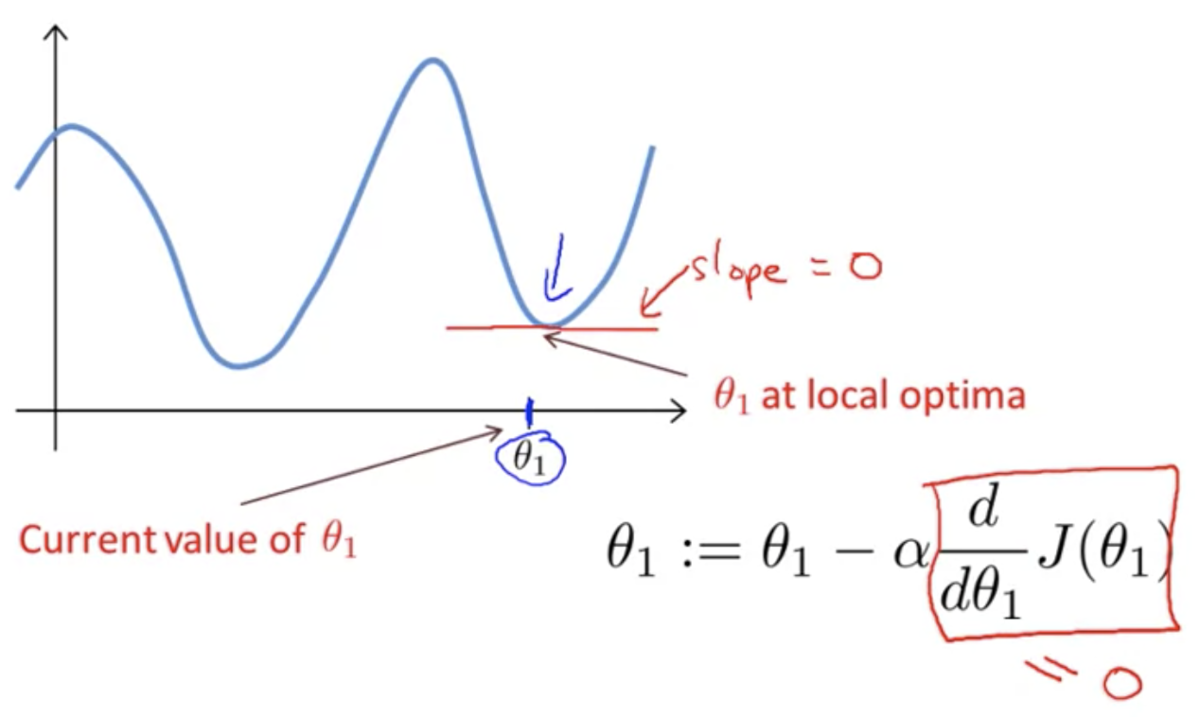
数学的表現：
- " $a := b$ "は $b$ を $a$ に代入することを意味する
- : 学習率 ()
  - 降下するステップの大きさを決める
- $\displaystyle{\frac{∂}{∂θ} _ jJ(θ _ 0, θ _ 1)}$ : 導関数項 (解説は先の章)
- , は同時に更新するように実装すること
  - 一方を更新した後、更新した値を使って他方を計算しないように

f:id:sasakino:20200822005126p:plain:w600

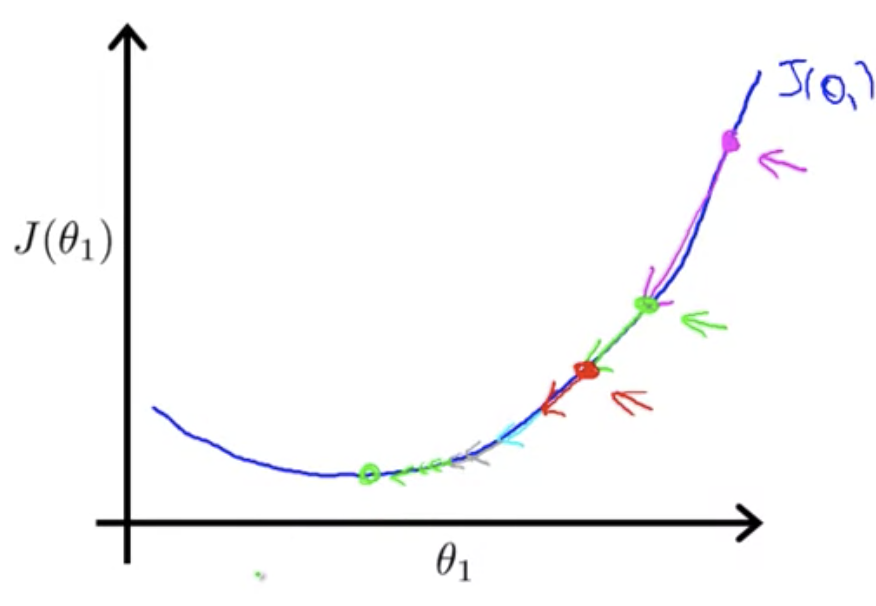
勾配降下法の直感的理解 (Gradient Descent Intuition)

目的関数のパラメータが $θ _ 1$ のみの場合の勾配降下法を考える
- $θ _ 1$ は実数 ( $θ _ 1∈$ R)
導関数項について：
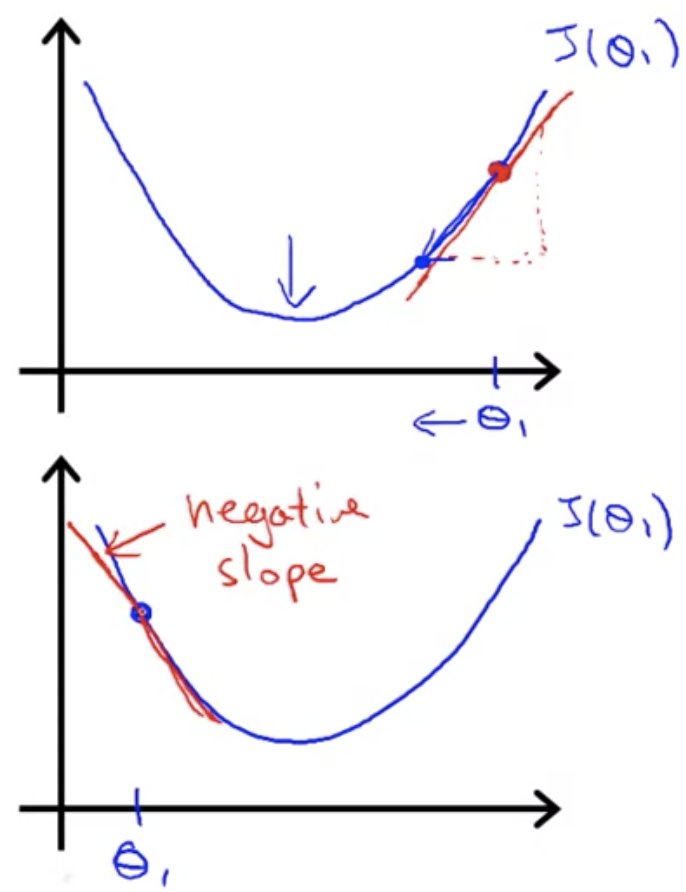
- 微分とは接線の傾きを調べること
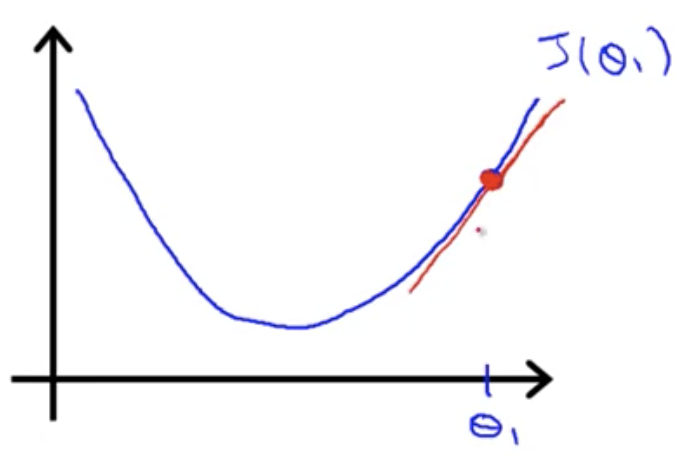
- 傾きが正か負かによって $θ _ 1$ の更新方向が決まる
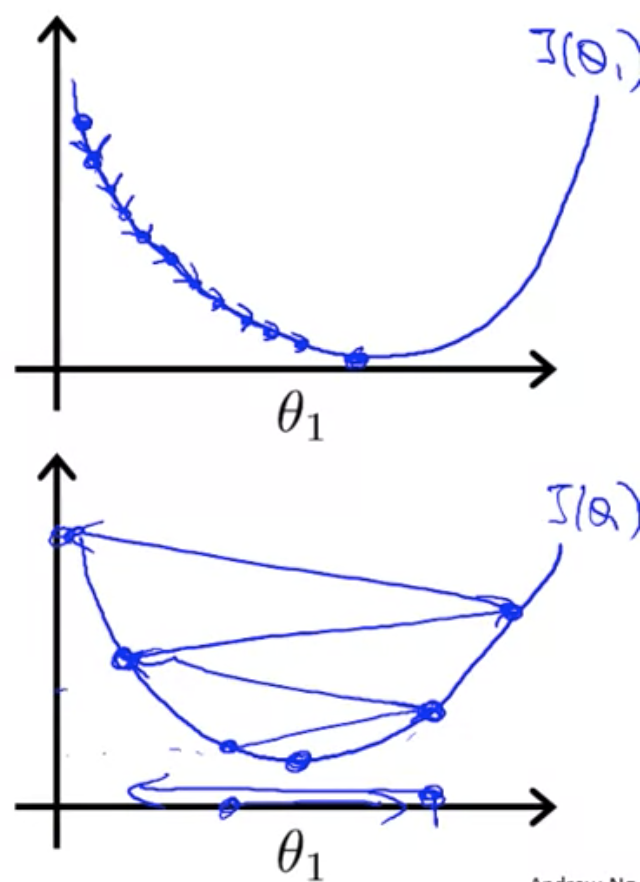
- 学習率 $α$ が小さすぎると収束まで時間がかかり、大きすぎると収束しなかったり発散してしまったりする
- $θ _ 1$ が局所的最適解で初期化されると、傾きが0になり更新されない

f:id:sasakino:20200822014539p:plain:w400

$θ _ 1$ を適切な学習率で更新するたびに、傾きは小さくなり(最急降下法のステップが小さくなり)、最終的に(局所的)最小値に収束する

勾配降下法の線形回帰への適用 (Gradient Descent For Linear Regression)

導関数項の計算
偏微分計算の詳細 :

$\displaystyle{ \frac{∂}{∂θ _ j}J(θ _ 0, θ _ 1) = \frac{∂}{∂θ _ j} _ {j}\frac{1}{2m}\sum_{i=1} ^ {n}(h _ {θ}(x ^ {(i)})-y ^ {(i)}) ^ {2} \\ = \frac{1}{2m}\frac{∂}{∂θ _ j}\sum_{i=1} ^ {n}(h _ {θ}(x ^ {(i)})-y ^ {(i)}) ^ {2} \\ = \frac{1}{2m}\sum_{i=1} ^ {n}2(h _ {θ}(x ^ {(i)})-y ^ {(i)})\frac{∂}{∂θ _ j}(h _ {θ}(x ^ {(i)})-y ^ {(i)}) \\ = \frac{1}{m}\sum_{i=1} ^ {n}(h _ {θ}(x ^ {(i)})-y ^ {(i)})\frac{∂}{∂θ _ j}(θ _ 0+θ _ {1}x ^ {(i)}-y ^ {(i)}) \\ ここで \\ j=0 : \frac{∂}{∂θ _ 0}(θ _ 0+θ _ {1}x ^ {(i)}-y ^ {(i)}) = 1 \\ j=1 : \frac{∂}{∂θ _ 1}(θ _ 0+θ _ {1}x ^ {(i)}-y ^ {(i)}) = x ^ {(i)}\\ よって \\ j=0 : \frac{∂}{∂θ _ 0}J(θ _ 0, θ _ 1)= \frac{1}{m}\sum_{i=1} ^ {n}(h _ {θ}(x ^ {(i)})-y ^ {(i)})\\ j=1 : \frac{∂}{∂θ _ 1}J(θ _ 0, θ _ 1)= \frac{1}{m}\sum_{i=1} ^ {n}(h _ {θ}(x ^ {(i)})-y ^ {(i)})x ^ {(i)}\\ }$