第2週：複数の変数を使用した線形回帰【Coursera Machine Learningコース】

プログラミング課題の環境構築

Octaveをインストール
- 参考 : MacでOctaveの環境構築備忘録 - Qiita

多変量線形回帰 (Multivariate Linear Regression)

複数の特徴量 (Multiple Features)

複数の特徴量を使う場合を考える

f:id:sasakino:20200822154407p:plain:w400

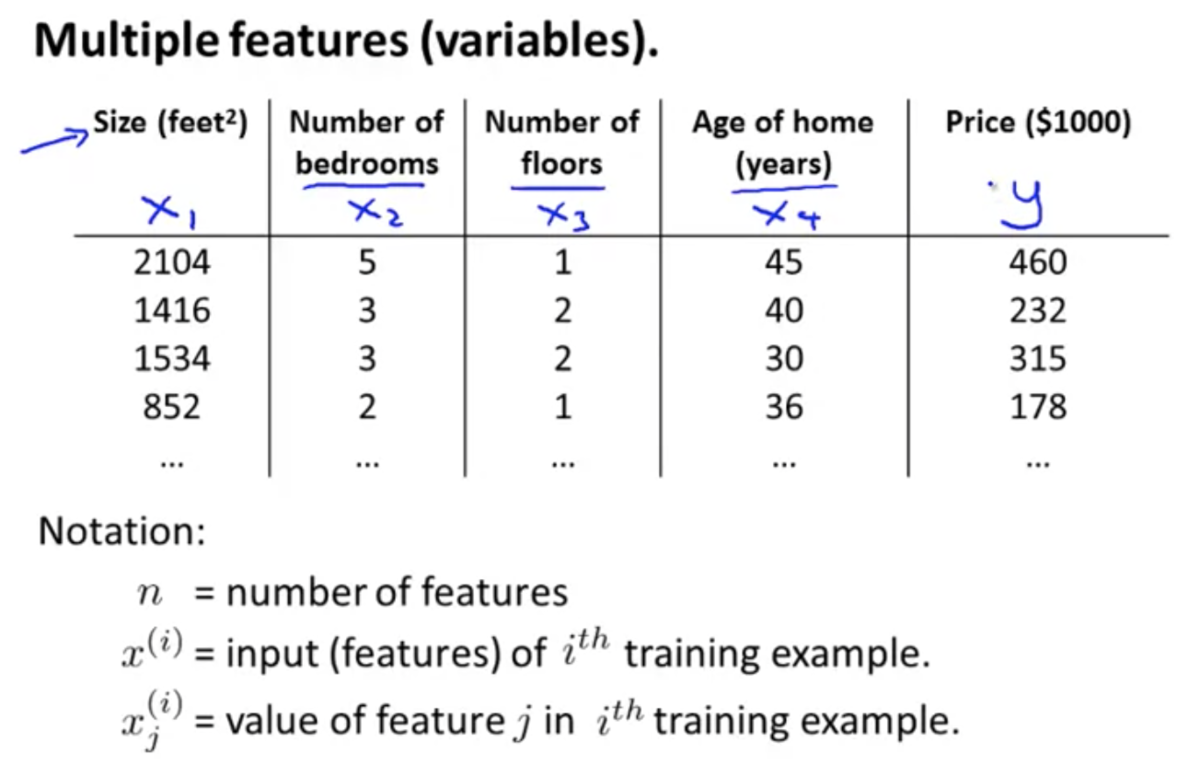
シンボル定義：
- $n$ : 特徴量の種類の数
- $x ^ {(i)}$ : $i$ 番目のトレーニングサンプル (ベクトル量)
- $x _j ^ {(i)}$ : $i$ 番目のトレーニングサンプルにある $j$ 番目の特徴量
$n = 4$ のときの仮説関数 $h _ θ(x)$ : $h _ θ(x)=θ _ 0+θ _ 1x _ 1+θ _ 2x _ 2+θ _ 3x _ 3+θ _ 4x _ 4$
- $x ^ {(i)} _ 0=1$ とおくと、 $h _ θ(x)=θ _ n x _ n$ とかける
  → $θ$ , $x$ はそれぞれn+1次元ベクトルなので、 $h _ θ(x)=θ^{T}x$ のようにベクトルの内積としてもかける
このように特徴量が複数ある線形回帰を、多変量線形回帰とも呼ぶ

複数の変数の勾配降下

複数の特徴量を持つ仮説関数に対してどのようにパラメータをフィットさせるか？
勾配降下法を多変量線形回帰に適用する場合を考える

仮説関数、パラメータ、目的関数について：

f:id:sasakino:20200822163728p:plain:w500

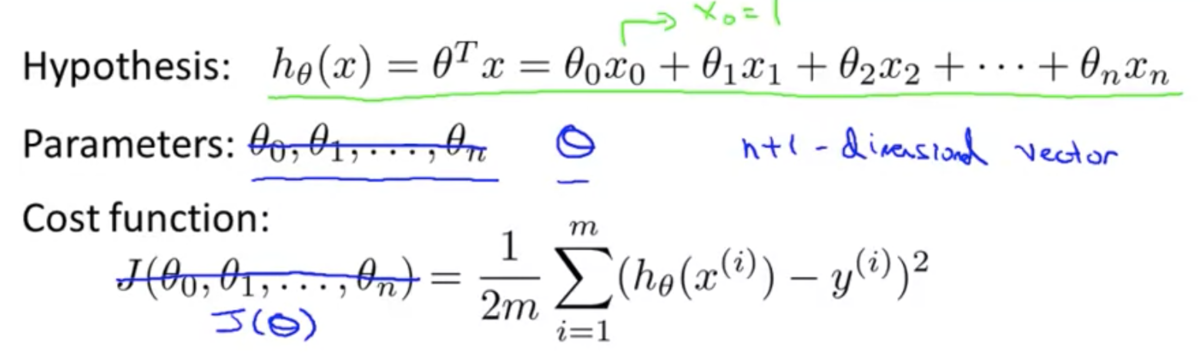
パラメータ $θ$ はn+1次元ベクトルとして考える
$J$ はベクトル $θ$ を引数にとる関数として考える

勾配降下法は以下のように一般化される

f:id:sasakino:20200822164232p:plain:w300

実践における勾配降下法１ - 特徴量スケーリング

勾配降下法は各特徴量のスケールが似ていると早く収束する

事前に各特徴量に正規化を施してスケールを合わせておくことで、収束までの時間を短縮できる
多くの場合、特徴量が $-1 ≦ x _ i ≦ 1$ の範囲をとるように正規化する

平均ノーマライゼーション (Mean normalization)

正規化の方法のひとつ

i 番目の特徴量 $x _ i$ に対して以下の計算をする (ただし $x _ 0$ には適用しない)

$\displaystyle{x _ i := \frac{x _ i - μ _ i}{s _ i}}$

$μ _ i$ : 特徴量 $x _ i$ の平均値
$s _ i$ : 特徴量 $x _ i$ の最大値 - 最小値

実践における勾配降下法２ - 学習率

勾配降下法が正しく機能しているか確認する方法

横軸に勾配降下法のイテレーション回数、縦軸に目的関数 $J$ の値をとって、 $J$ の値の推移をプロットする

f:id:sasakino:20200823001922p:plain:w300

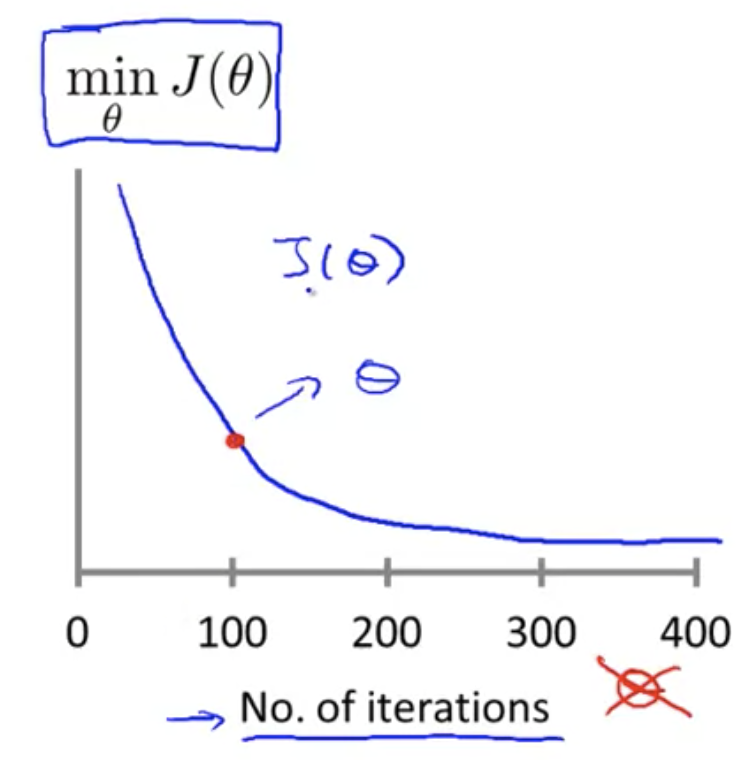
勾配降下法がちゃんと機能していれば、 $J$ の値は減少していく
必要なイテレーション回数を事前に知ることは難しい
そのためこのようにプロットして確認することが必要
変化率が小さくなってきたらもう収束しているということ
例えば、一回のイテレーションで $J$ が $10^{-3}$ しか減少しなかったら収束とみなすことで、自動収束テストも可能 (ただしこの閾値を決めるのもまた難しい)
もし $J$ が増加しているようだったら、オーバーシュートを起こしているのかもしれない
その場合は、学習率 $α$ を小さくすることで改善できる
（もちろんコーディングミスも疑うべき）
また、 $J$ が増減を繰り返すような場合もある
その場合も学習率 $α$ を小さくすることで改善できる

学習率の選び方

ある程度スケールの異なるいくつかの学習率 $α$ で $J$ のプロットを行い、 $J$ が順調に減少していそうな学習率を選ぶ
これを何度か繰り返す

特徴量と多項式回帰 (Features and Polynomial Regression)

特徴量の選び方について

例えば住宅価格を予測するために『間口の広さ』と『奥行き』という２つの特徴量を持っているとする

この場合、この２つの特徴量をそのまま使うのではなく、２つの掛け合わせて『敷地面積』というひとつの特徴量を作り出してもいい

多項式回帰について

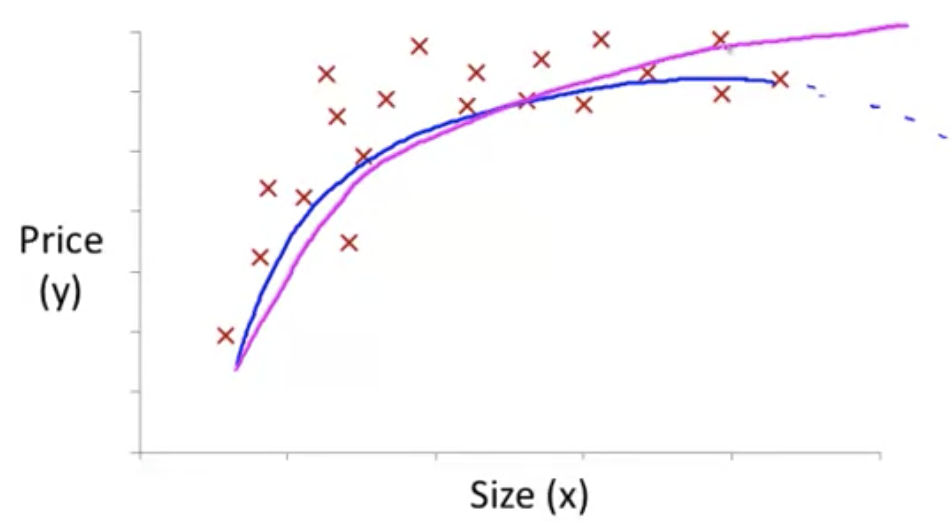
たとえば以下の図のようなデータは、線形回帰だとうまくフィットしなさそうに見える

f:id:sasakino:20200823095422p:plain:w400

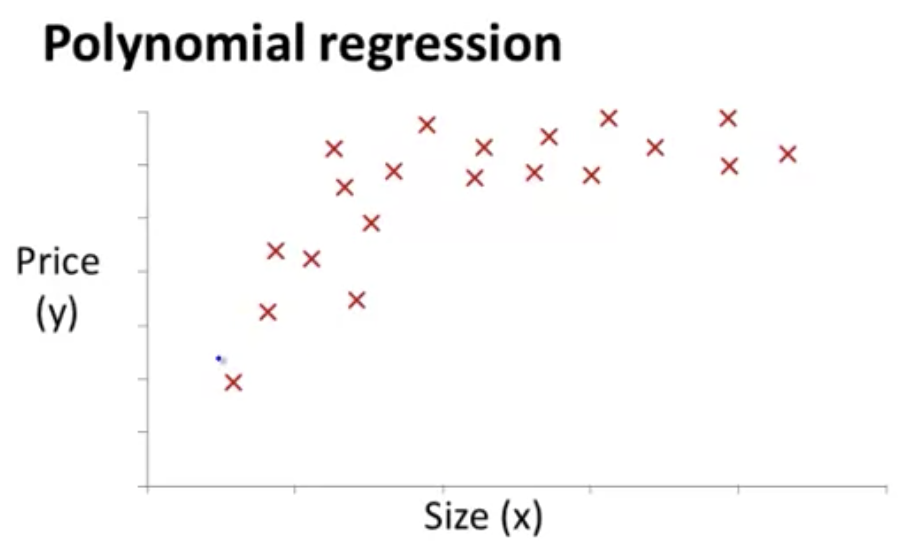
このような場合、例えば $h _ θ(x) = θ _ 0 + θ _ 1x + θ _ 2x ^ 2$ のような二次関数を仮説として使うことができる

ただし、二次関数はいずれ弧を描いて下降するため、住宅価格の予測には適さないかもしれない

代わりに $h _ θ(x) = θ _ 0 + θ _ 1x + θ _ 2x ^ 2 + θ _ 3x ^ 3$ のような関数を選べば降下しなくなる

データのフィッティングの仕方はこれまでと変わらず、
$h _ θ(x) = θ _ 0 + θ _ 1x + θ _ 2x ^ 2 + θ _ 3x ^ 3$
の $x$ , $x ^ 2$ , $x ^ 3$ をそれぞれ
$x' _ 1 = x$
$x' _ 2 = x ^ 2$
$x' _ 3 = x ^ 3$
とおけば、これまで見てきたような
$h _ θ(x) = θ _ 0 + θ _ 1x' _ 1 + θ _ 2x' _ 2 + θ _ 3x' _ 3$
という式として考えることができる

住居の価格としてフィッティングしそうな関数を挙げるとすれば以下のようなもの
$h _ θ(x) = θ _ 0 + θ _ 1(size) + θ _ 2\sqrt{(size)}$
f:id:sasakino:20200823113302p:plain:w300

パラメータの解析的計算 (Computing Parameters Analytically)

正規方程式 (Normal Equation)

目的関数を最小化する方法として、勾配降下法の他に、正規方程式を解くという方法がある
正規方程式を使ってパラメータを解析的に解くと、一度に全てのパラメータを求めることができる

目的関数を最小化するには
$\frac{∂}{∂θ _ j}J(θ) = 0$ (for every $j$ )
を解けばいい

すると
$θ = (X ^ {T}X) ^ {-1}X ^ {T}y$
を得る　これが正規方程式
（ $(X ^ {T}X) ^ {-1}$ は逆行列）

XとYの例
f:id:sasakino:20200823121734p:plain:w400

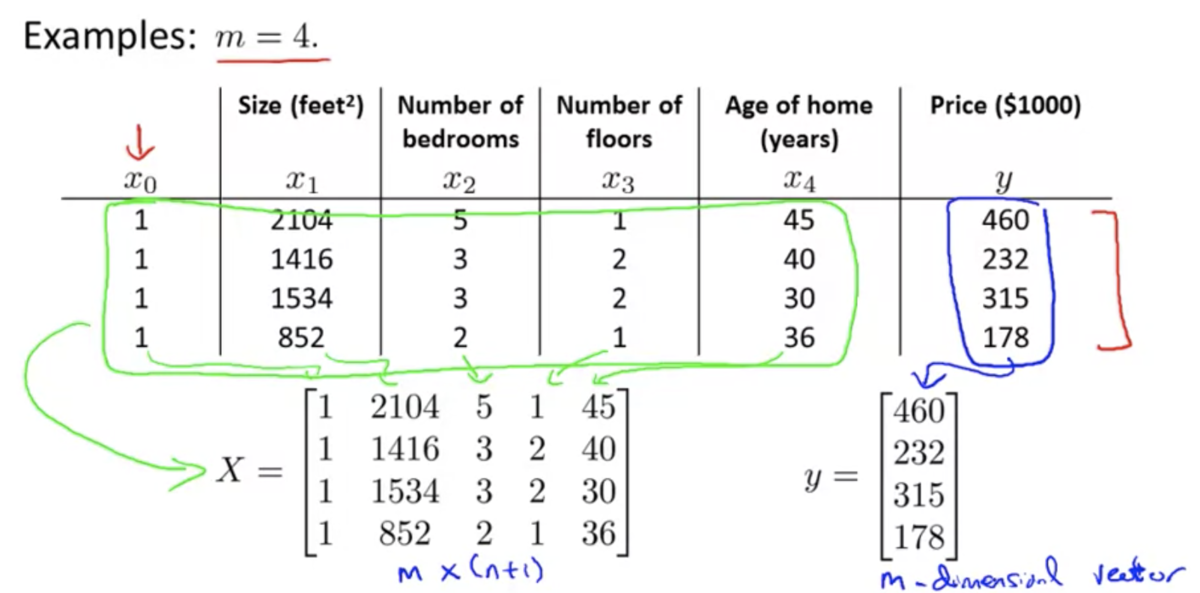
正規方程式を使う場合、特徴量スケーリングは必要ない

正規方程式は、線形回帰では使えるが、より複雑な学習アルゴリズム（ロジスティック回帰など）ではうまく機能しない

勾配降下法と正規方程式のメリット・デメリット

勾配降下法

メリット
- 特徴量の種類の数が多くても機能する
デメリット
- 適切な学習率 $α$ を試行錯誤して見つける必要がある
- 多くのイテレーションが必要

正規方程式

メリット
- 学習率 $α$ を必要としない
- イテレーションを回す必要がない
デメリット
- 特徴量の種類の数が多いと計算コストが跳ね上がる
  - 逆行列計算の計算オーダーは $O(n ^ 3)$ らしい
  - 経験則として、n = 100 ~ 1000程度なら全然大丈夫、n = 10000くらいになると悩み始めるとのこと

正規方程式の非可逆性 (Normal Equation Noninvertibillity)

補足的な内容らしいのでとばした

ささきのブログ

日記、技術メモ、勉強記録など。