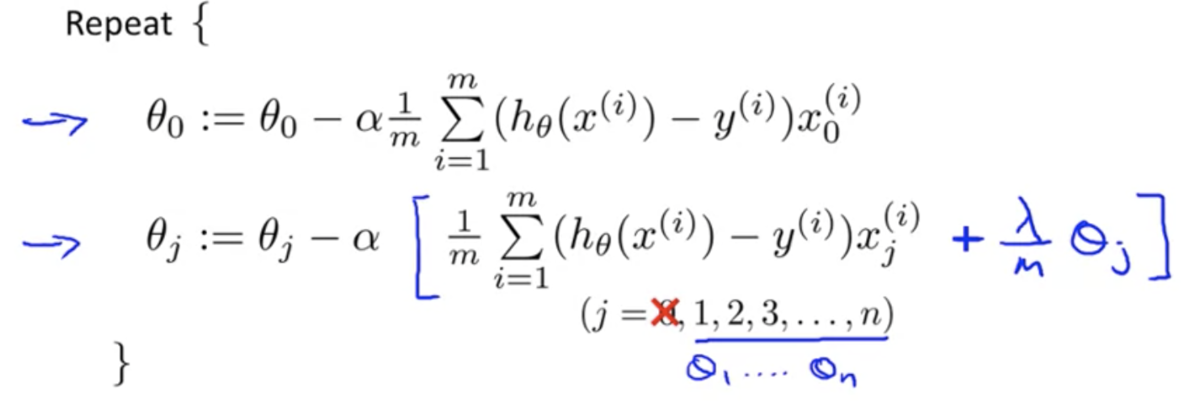第3週:ロジスティック回帰【Coursera Machine Learningコース】
テーマ
分類と表現 (Classification and Representation)
分類 (Classification)
分類問題の例:

目的変数が0か1かで判別する

線形回帰ではデータをうまく2つに分けることができない
また、分類問題では or
であるべきなのに、
線形回帰の仮説では or
も有り得てしまう
そのため線形回帰は分類問題に適さない
仮説表現 (Hypothesis Representation)
どのような関数を仮説の表現に用いるか
分類問題では となるような仮説が欲しい
線形回帰の仮説の形は だった
ロジスティクス回帰では、 のような形になる
ここで は
と定義される
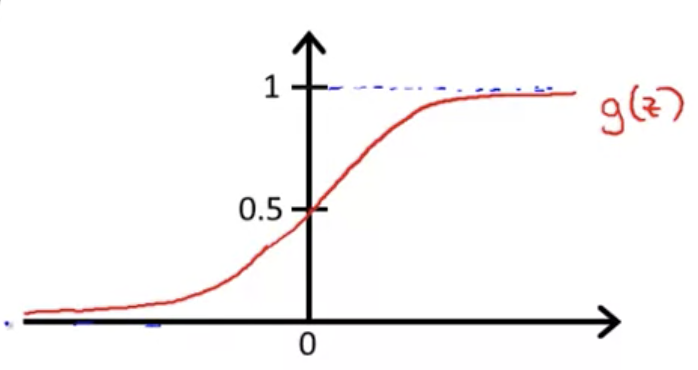
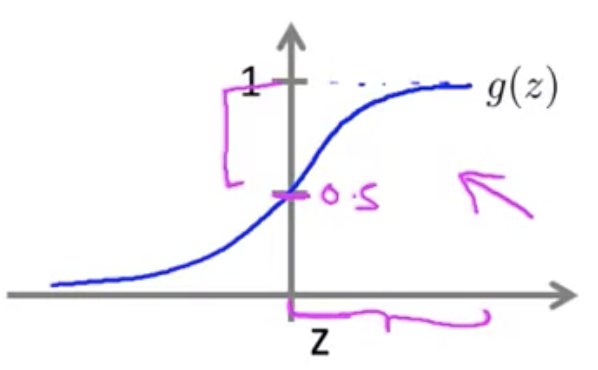
この関数はシグモイド関数、またはロジスティクス関数と呼ばれるもの
ロジスティクス関数は以下の図に示すように、 になる性質をもつ
そのため、分類問題に求められる仮説の条件を満たす
この に
を代入すると、
となる
これがロジスティクス回帰の仮説
仮説の出力の解釈について
ロジスティクス回帰の仮説 の出力は、
入力 に対する結果
が 1 になる確率を表している
例えば だったら、その入力
は70%の確率で 1 に分類されるということ
これを形式化すると次の式のように書ける
(θ でパラメータ化された x が与えられたときに y = 1 である確率、と読む)
決定境界 (Decision Boundary)
決定境界と呼ばれるものを知ることでロジスティクス回帰が何を計算しているかを理解する
のとき
のとき
とすると、ロジスティクス回帰では のとき必ず y = 1 となる (逆も成り立つ)
つまり、 なら
,
なら
となる
ここで、下図のようなデータセットの分布があったとする
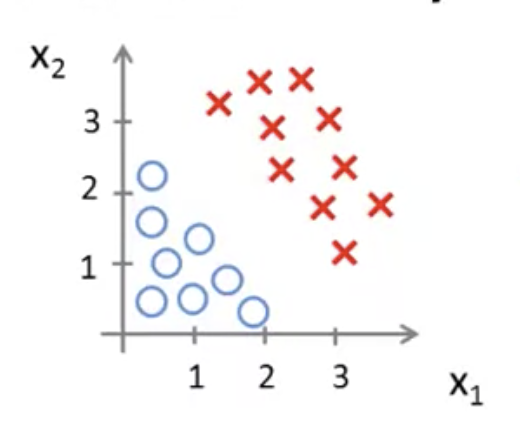
仮説として次のような式を用いる
このとき、最適なの値が
だったとする
ロジスティクス回帰では なら
なので、
この場合は
⇒ のとき
となる
という直線を図に加えると以下のようになる
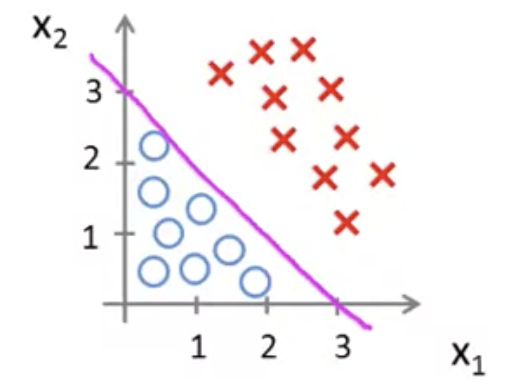
は直線の上の領域を表す
つまり y = 1となる領域
逆に、直線の下の領域は y = 0 の領域となる
このようにy = 1 の領域とy = 0の領域を分ける直線を決定境界と呼ぶ
なお、決定境界はデータセットの性質ではなく、仮説とパラメータの性質である
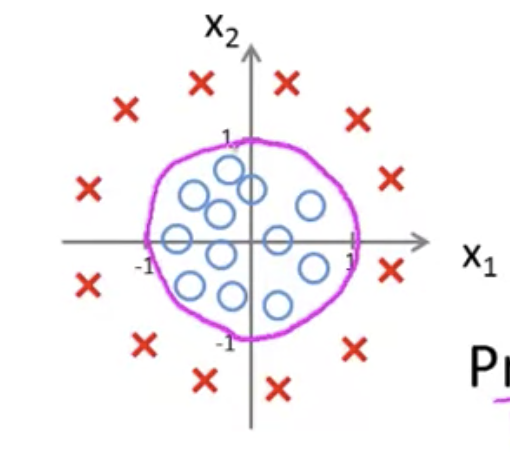
例としてデータセットの分布が以下の図のような場合、
のようにしておけば、
パラメータを適切に最適化することにより円の方程式を得ることができる
さらに高次の多項式では、より複雑な決定境界を得ることも可能
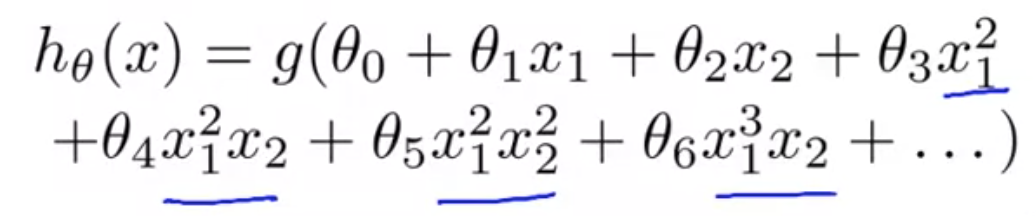
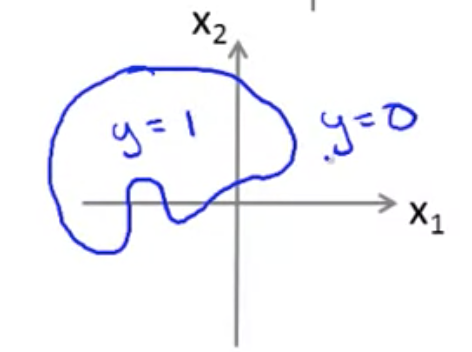
ロジスティック回帰モデル (Logistic Regression Model)
目的関数 (Cost Function)
今まで見てきたコスト関数を次のように変形する(1/2の場所を移動)
ここで、二乗誤差の項を次のようにおく
代入すると以下のようになる
は文字通り、学習アルゴリズムが値を出力する際、
予測が で実際のラベルが
だった場合に発生するコスト(費用)であると解釈する
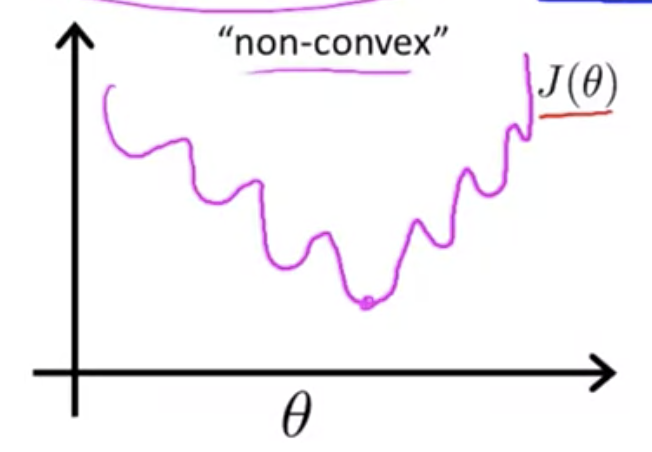
線形回帰の場合は二乗誤差をコストとして用いることができたが、
ロジスティクス回帰の場合、二乗誤差を使うと目的関数は下図のように非凸関数になってしまい、
勾配降下法で最適解を求めることが困難になってしまう(勾配降下法は凸関数の場合に効果を発揮する)
そこで、ロジスティクス回帰では次のようなコスト関数を用いる
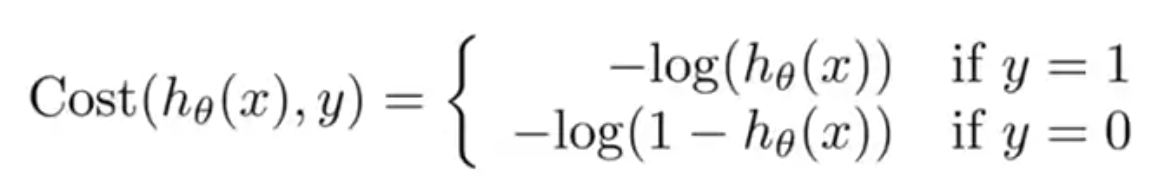
それぞれの関数では が
の範囲に収まるため、以下の図のようなプロットになる
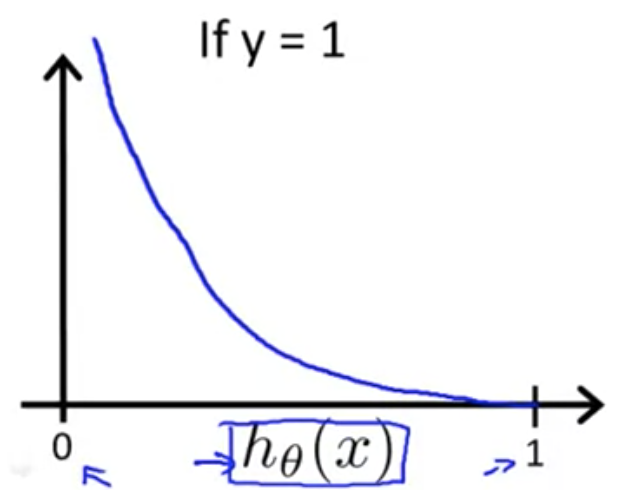
のときは
が 0 に近くほど、
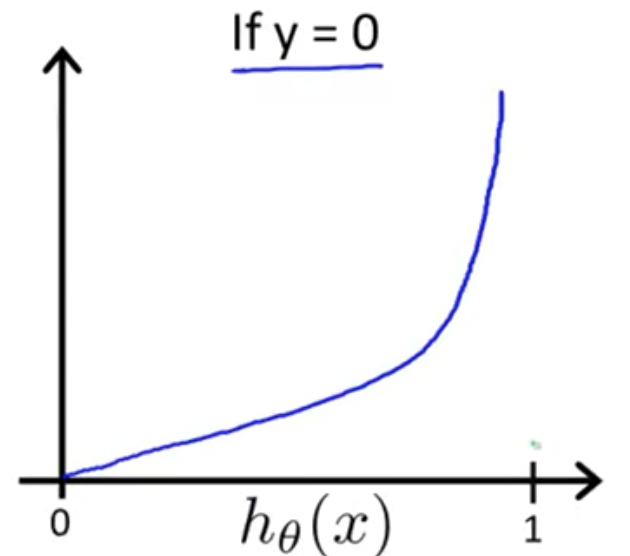
また のときは
が 1 に近くほど、
コストが無限大に近づいていることがわかる
簡素化された目的関数と勾配降下法 (Simplified Cost Function and Gradient Descent)
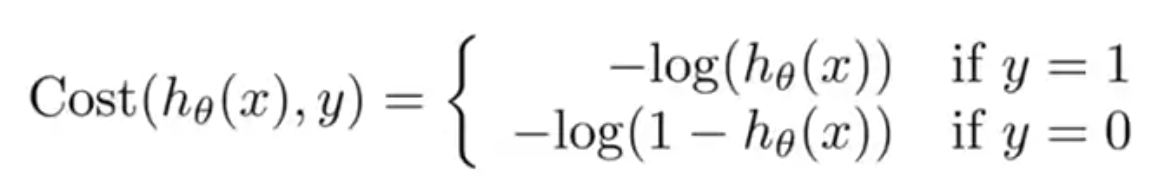
この式は、以下のように1行にまとめることができる
よって、ロジスティクス回帰の目的関数は以下のようになり、
パラメータ を最適化するにはこの
を最小化すればいい
を最小化には勾配降下法を用いる
勾配降下法のアルゴリズムは以下のようなもの
偏微分項を計算すると、線形回帰のときと同様の形になる
( はロジスティクス回帰のもの)
高度な最適化 (Advanced Optimization)
勾配降下法ではと
の偏微分を計算するが、
この2つを用いることで、別の(より高度な)最適化アルゴリズムも利用できる
- 共役勾配法 (Conjugate gradient)
- BFGS
- L-BFGS
これらに共通する特徴として、以下がある - 学習率αを手動で求める必要がない - 多くの場合、勾配降下法より高速
ただし、勾配降下法と比べて複雑なため、理解しようとすると難しい
これらを使うときは自前で実装するのではなく、機械学習ライブラリを使うべき
最適化手法のOctaveによる実装方法解説あり
Ovtaveのインデックスは1オリジンなので注意
多クラス分類 (Multiclass Classification)
one-vs-all (one-vs-rest) 分類というアルゴリズム →多クラス分類をいくつかの2クラス分類に分割して考える
例:クラスA, B, Cという3クラスに分類する問題 → 以下の3種類の2クラス分類に分割する ・クラスAとそれ以外の2クラス分類 ・クラスBとそれ以外の2クラス分類 ・クラスCとそれ以外の2クラス分類
実際に推測を行うときは、入力に対して、上記で得られた各分類器でそれぞれ推測を行い、もっとも確率の高い分類器の結果を返す
Solving the Problem of Overfitting
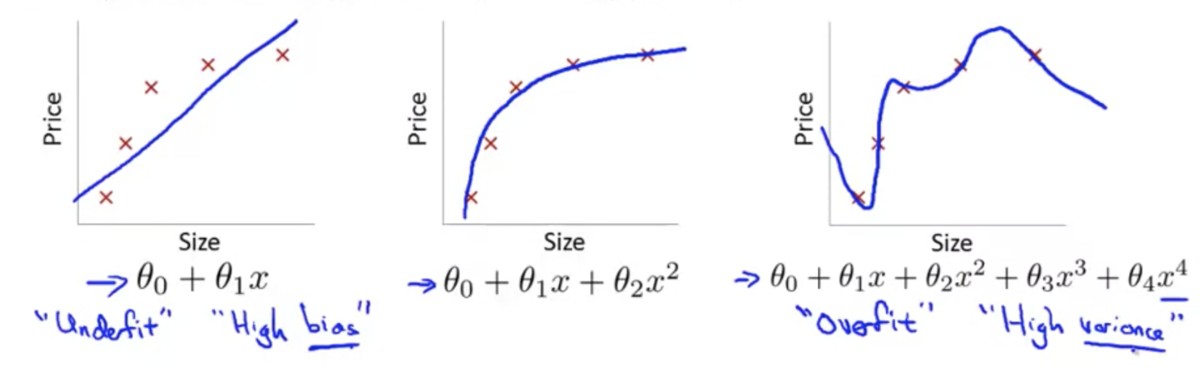
The Problem of Overfitting
オーバーフィッティング(過学習)問題とは
学習モデルが、データセットにはよく適合するが、データの予測には適さない状態になってしまうこと
このような状態をハイバリアンスとも表現する
線形回帰の例(3枚目がオーバーフィッティング):
ロジスティック回帰の例(3枚目がオーバーフィッティング):
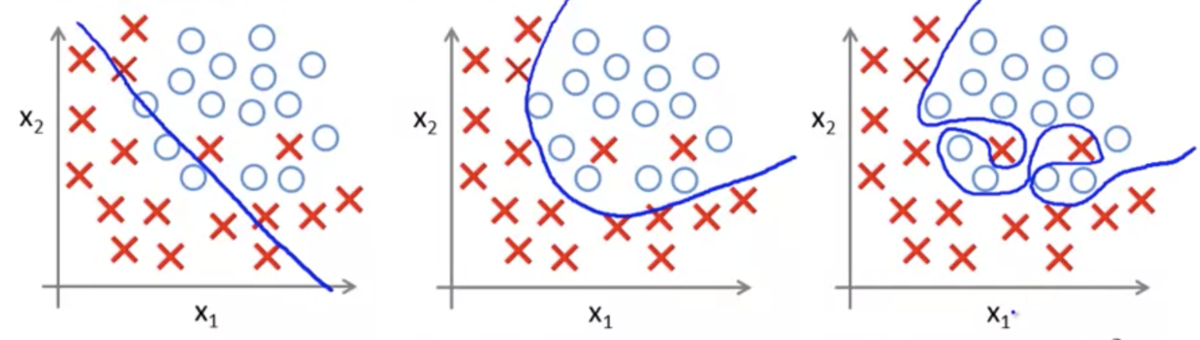
オーバーフィッティングが起きてしまったときの対応策
特徴量の種類を減らすデメリットとして、事前に重要な特徴量を知ることはできないため、重要な特徴量まで除外してしまう可能性があること
目的関数 (Cost Function)
パラメータθを小さく保つことで、よりシンプルな仮説となり、オーバーフィッティングしにくくなる
例えば下図のように、線形回帰の目的関数に正則化項を加えることで、θを小さく保つことができる→正則化
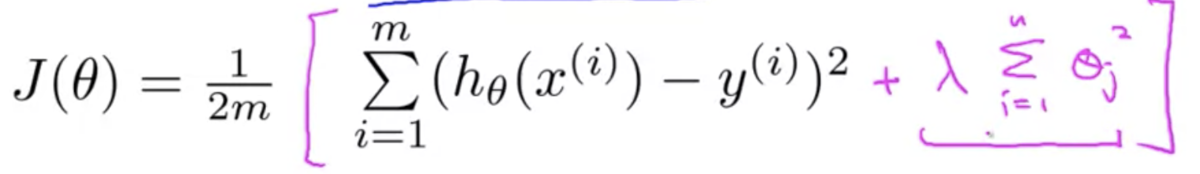
目的関数を最小化するには、正則化項が小さくなければならず、
正規化項を小さくするには、θを小さくしなけらばならない
→θを小さく保つことができる
ただし、正則化項のλがあまりに大きすぎると、各θはほぼゼロになる
すると、仮説が特徴量の影響をほぼ受けなくなってしまい、アンダーフィッティング状態に陥る
その場合、仮説はの形に近づき、プロットは下図のようになる

正則化された線形回帰 (Regularized Linear Regression)
正則化を取り入れた目的関数を勾配降下法で最適化する際は、以下のようにの場合とそれ以外とで場合分けをする
後者は正則化項が含まれた目的関数を偏微分しているので式の形が一部変わっている
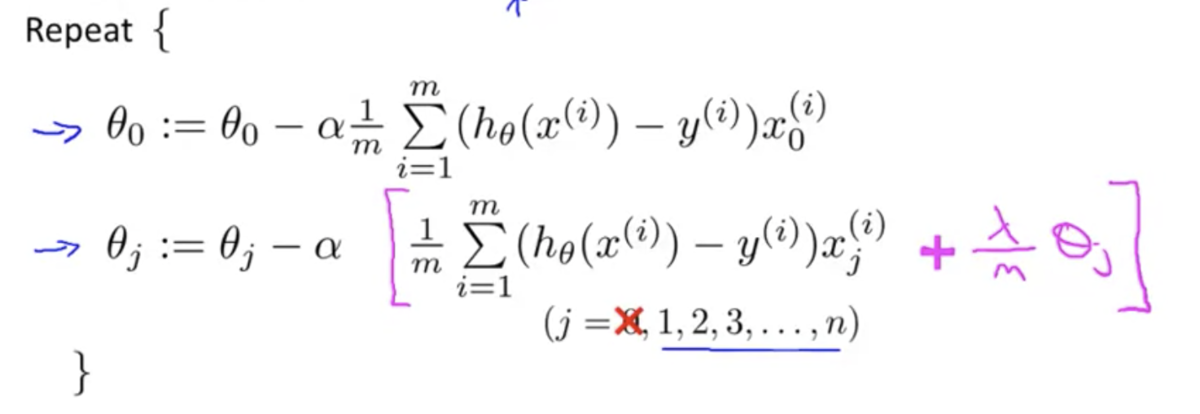
また、に関わる項をひとつにまとめると以下のようになる
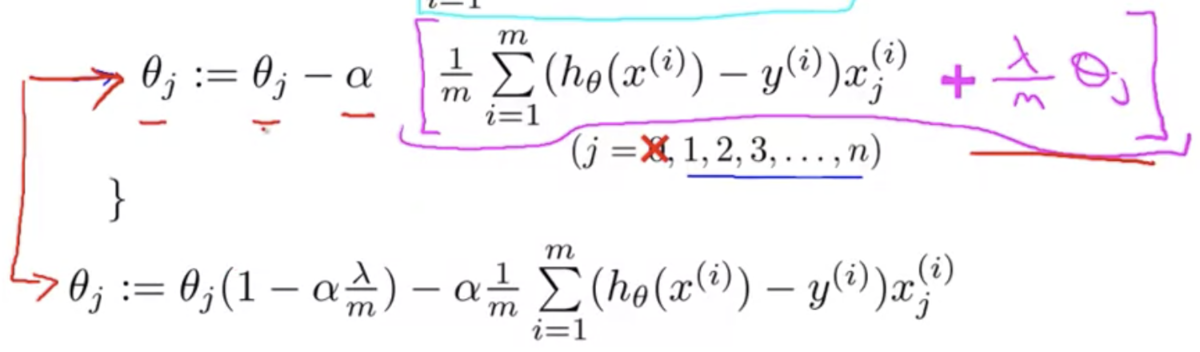
は通常 1 よりやや小さい値になる
なぜなら、学習率 α は正の小さな値を設定し、m は大きな値をとるから
1 より少しだけ小さい数字を に乗じるので、
の値は少しだけ小さくなる
なので、正則化項のある目的関数の勾配降下法では、各イテレーション毎に を少しだけ小さくし、あとは正則化項がない場合と同様のアップデートを施す
正規方程式の場合は、θ を求める式が以下のように変わる
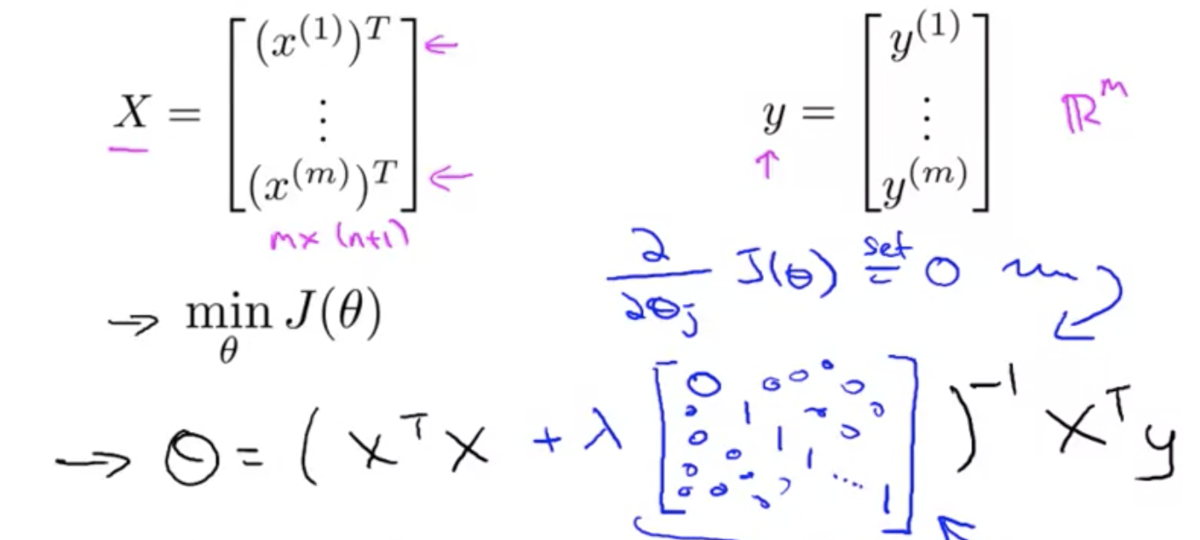
正則化されたロジスティック回帰 (Regularized Ligistic Regression)
ロジスティック回帰に正則化を適用する場合も、だいたいは線形回帰の場合と同じ
目的関数は以下のようになる
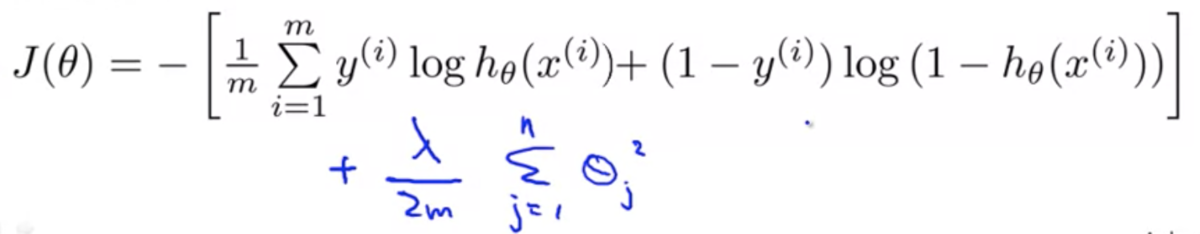
勾配降下法は以下のようになる