第5週：ニューラルネットワーク：学習【Coursera Machine Learningコース】

Cost Function and Backpropagation

Cost Function

シンボル定義：
L ... ネットワーク内のレイヤー数
$s _ l$ ... レイヤー $l$ にあるユニット数 (バイアスユニットは除く)
K ... 分類問題のクラス数

２クラス分類なら $h _ θ(x)∈R$ , $s _ L = 1$ , $K = 1$

多クラス分類なら $h _ θ(x)∈R ^ K$ , $s _ L = K$ (K ≧ 3)

ロジスティック回帰のときのコスト関数は以下。
f:id:sasakino:20200916232839p:plain:w550

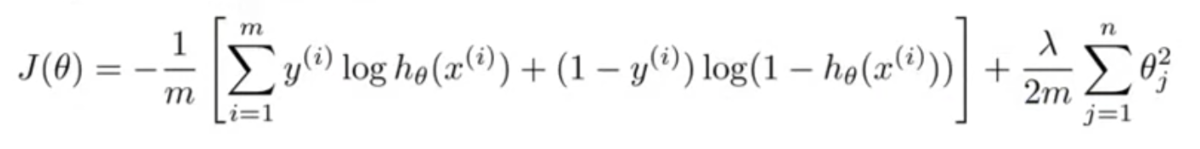
ニューラルネットワークでは以下のようになる。
f:id:sasakino:20200916232925p:plain:w550

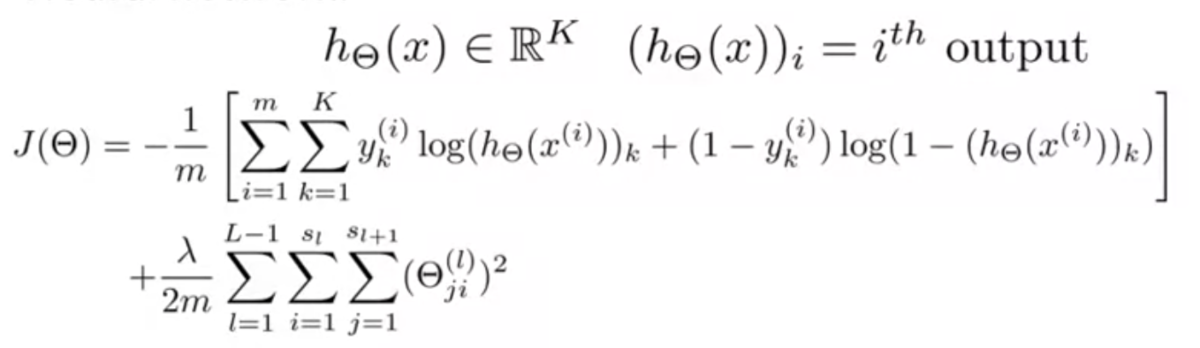
$i$ はユニットがK個あるうちの何番目かを表す添字。

ロジスティック回帰のコスト関数との違いは、ユニットK個分の和をとっていること。

正則化項はぱっと見複雑に見えるが、そんなに難しくない。

$l$ , $i$ , $j$ はそれぞれ、 $l$ 層目の $i$ 番目のユニットの
$j$ 番目の特徴量の重みを取り出すために使われている。

つまり、ネットワーク全体の重みの二乗和をとっているということ。

Backpropagation Algorithm

ニューラルネットワークでも、これまで同様、コスト関数とその微分が必要。
つまり、 $J(Θ)$ の他に、 $\displaystyle{\frac{∂}{∂Θ _ {ij} ^ {(l)}}J(Θ)}$ が必要。

この微分計算のために誤差逆伝搬法（Backpropagation）を使う。

誤差逆伝搬法は、レイヤ $l$ にあるノード $j$ 番目の誤差 $δ _ j ^ {(l)}$ を求めるイメージ。
ニューラルネットワークでは各レイヤにアクティベーション $a _ j ^ {(l)}$ が存在するが、
このアクティベーションが、期待される値からどれだけずれているかを求めていく。

具体的には以下のような計算をする。
レイヤ $L = 4$ で、トレーニングセットx, yがそれぞれ1つずつしかない場合を考えると

出力層 : $δ ^ {(4)} = a ^ {(4)} - y$

隠れ層 : $δ ^ {(3)} = (Θ ^ {(3)}) ^ T δ ^ {(4)} .* g'(z ^ {(3)})$

隠れ層 : $δ ^ {(2)} = (Θ ^ {(3)}) ^ T δ ^ {(3)} .* g'(z ^ {(2)})$

上式の $δ ^ {(l)}$ , $a ^ {(l)}$ , $y$ , $Θ ^ {(l)}$ , $z ^ {(3)}$ はそれぞれベクトル。
$.*$ という演算子は、要素ごとの積を表している。

$g'(z ^ {(3)})$ というのは、アクティベーション関数の $g$ を入力値が $z ^ {(3)}$ のところで微分した値。
これを計算すると、 $a ^ {(3)} .* (1 - a ^ {(3)})$ になる。

なお、レイヤ1(入力層)にはアクティベーションがない（入力値）ので、 $δ$ も存在しない。

このように、誤差 $δ$ を出力層から始めてレイヤを遡りながら
計算していくので、誤差逆伝搬法と呼ばれている。

正規化項を無視すると、これらの誤差 $δ$ を使って、 $\displaystyle{\frac{∂}{∂Θ _ {ij} ^ {(l)}}J(Θ)}$ は以下のように計算できる。
$\displaystyle{\frac{∂}{∂Θ _ {ij} ^ {(l)}}J(Θ)} = a _ j ^ {(j)} δ _ i ^ {(l+1)}$

以上の計算を、トレーニングセットが複数ある場合（{( $x ^ {(1)}$ , $y ^ {(1)}$ ), ..., ( $x ^ {(m)}$ , $y ^ {(m)}$ )}）で考える。

まず、 $Δ _ {ij} ^ {(l)} = 0$ とおく。これは後ほど偏微分項を累積するために使う。

次に $j = 1$ から $i = m$ までのループの中で（つまり各トレーニングセットに対して）以下の計算をする。
・ $a ^ {(1)} = x ^ {(i)}$ （入力層）
・フォワードプロパゲーションにより $a ^ {(l)}$ を算出 ( $l = 2, 3, ..., L$ )
・出力層の誤差 $δ ^ {(L)} = a ^ {(L)} - y ^ {(i)}$ を計算
・バックプロパゲーションにより $δ ^ {(L-1)}, δ ^ {(L-2)}, ..., δ ^ {(2)}$ を計算
・ $Δ ^ {(l)} := Δ ^ {(l)} + δ ^ {(l+1)} (a ^ {(l)}) ^ T$ で偏微分項を累積する

最後に、ループを抜けたのち、以下のように正規化項の計算をする。
・ $\displaystyle{D _ {ij} ^ {(l)} := \frac{1}m Δ _ {ij} ^ {(l)} + λθ _ {ij} ^ {(l)}}$ （ $j ≠ 0$ の場合）
・ $\displaystyle{D _ {ij} ^ {(l)} := \frac{1}m Δ _ {ij} ^ {(l)}}$ （ $j = 0$ , つまりバイアス項の場合）

以上で、ニューラルネットワークのコスト関数の偏微分は次のように計算できる。
$\displaystyle{\frac{∂}{∂Θ _ {ij} ^ {(l)}}J(Θ)} = D _ {ij} ^ {(l)}$

Backpropagation Intuition

逆伝搬は線形回帰やロジスティック回帰に比べると、数学的にクリーンでもシンプルでもない。
なので直感的には理解しにくいかもしれない。

直感的に理解できなくても、使い方さえ覚えれば問題ない。
課題をこなすことで、逆伝搬の実装方法は分かるようになる。ひとまずそれでいい。

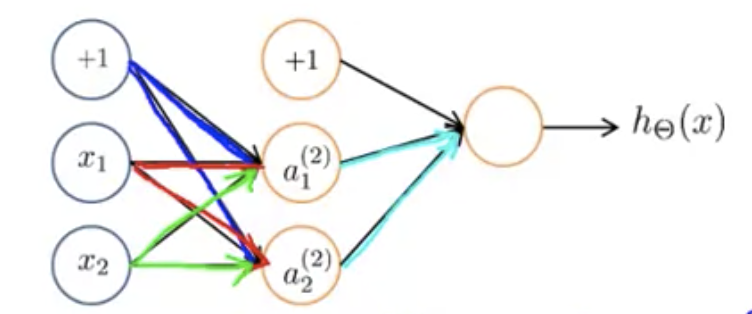
下図のようなニューラルネットワークがあるとする。
f:id:sasakino:20200925212049p:plain:w400

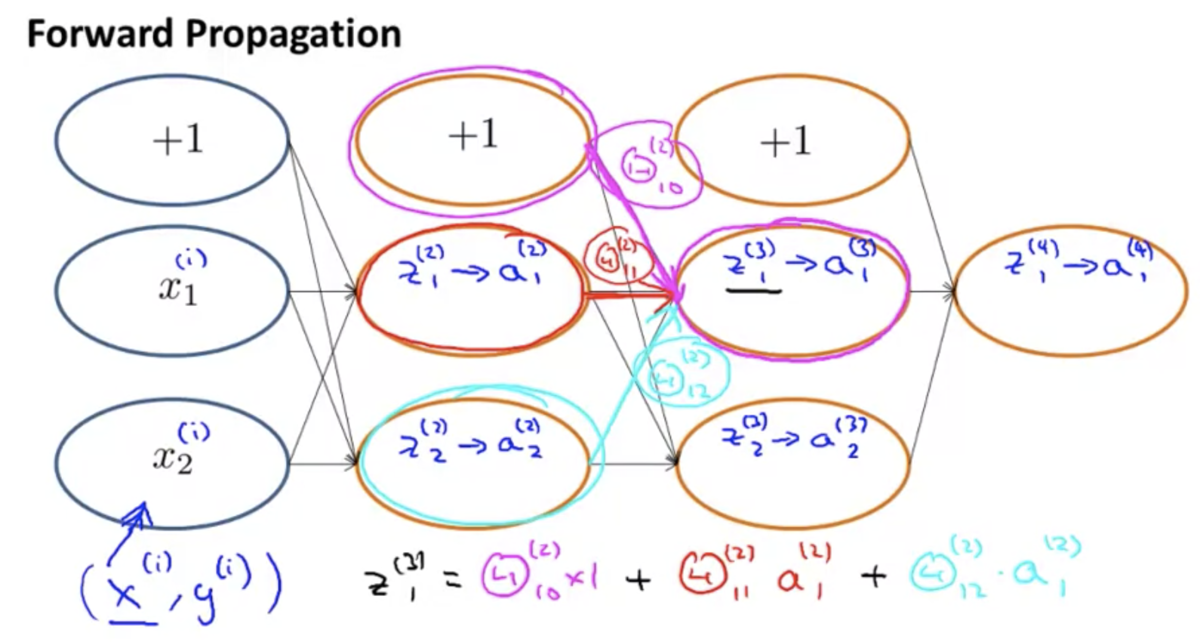
順伝搬において、あるノードへの入力は、ひとつ前のレイヤーの各ノードの出力に重みをかけたものの和になっている。

逆伝搬の計算も、これと似たプロセスになっている。
違いは、計算が左から右に流れるか、右から左に流れるか。

逆伝搬のコスト関数について、データセットのうち $x ^ {(i)}$ と $y ^ {(i)}$ だけに着目し、出力ユニットはひとつだけとして、正規化項を無視すると、以下のようになる。
f:id:sasakino:20200925212733p:plain:w400

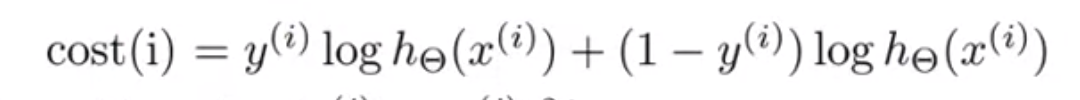
このコスト関数がやっているのは、誤差の２乗と似たような役割。
そのため、感覚的な理解としては、
$cost(i) ≒ (h _ Θ (x ^ {(i)}) - y ^ {(i)}) ^ 2$
のように近似して考えてもよい。

では、これを前提として、逆伝搬が何をやっているか。

逆伝搬は、 $δ _ j ^ {(l)}$ を計算している。
これは、 $l$ 番目のレイヤーにある $j$ 番目のユニットのアクティベーション $a _ j ^ {(l)}$ の値の「誤差」と捉えることができる。

正式には、 $\displaystyle{ δ _ j ^ {(l)} = \frac{∂}{∂z _ j ^ {(l)}} cost(i)}$ を計算している。

直感的には以下のように理解すればよい。

$δ _ j ^ {(l)}$ の求め方は順伝搬とよく似ていて、前のレイヤーの各ユニットの誤差の重みつき和になっている。

例えば下図のように、出力層の誤差 $δ _ 1 ^ {(4)}$ は、正解データと出力値の差をとる。
$δ _ 1 ^ {(4)} = y ^ {(i)} - a _ 1 ^ {(4)}$
f:id:sasakino:20200926072443p:plain:w400

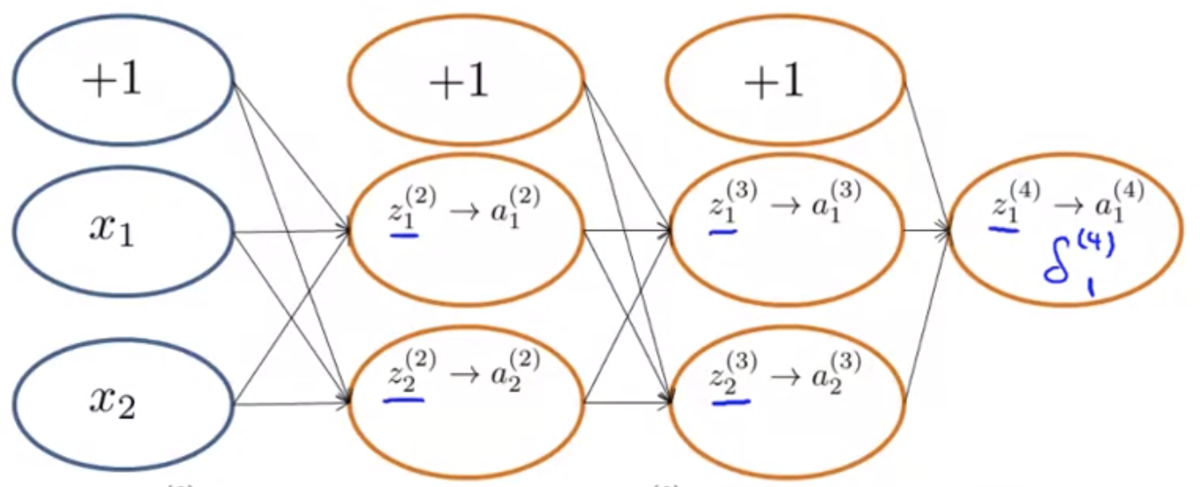
レイヤー２のユニット２の誤差 $δ _ 2 ^ {(2)}$ なら、下図のようになる。
f:id:sasakino:20200926072838p:plain:w500

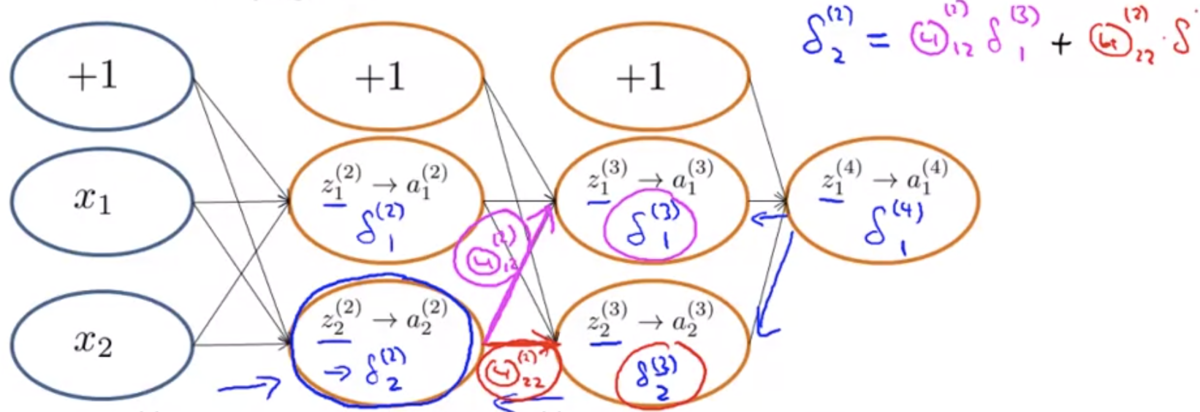
バイアスユニットについては誤差がないので無視してよい。

Backpropagation in Practice

Implementation Note: Unrolling Parameters

行列からベクトルへのパラメータのアンロールについて。
高度な最適化アルゴリズムを利用する際、これが必要になる。

Octaveで学習を走らせる際、以下のようなコードを書いてた。

function [jVal, gradient] = costFunction(theta)

...

optTheta = fminunc(@costFunction, initialTheta, options)

ここで、thetaやgradientはベクトルを期待している。
しかしニューラルネットワークにおいてこれらは行列になる。
そのため、行列からベクトルへのアンロールが必要になる。

例として、下図のようなネットワークを考える。
f:id:sasakino:20200926091842p:plain:w550

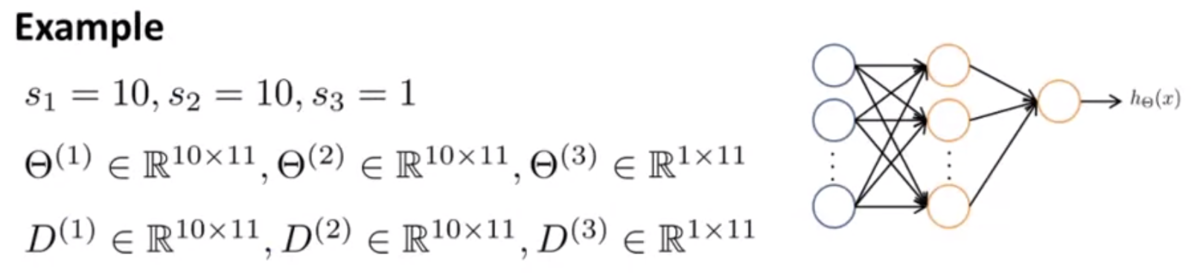
このとき、行列ΘやDをベクトルにアンロールするには、(Octaveの場合)以下のようなコードを書けばよい。
f:id:sasakino:20200926093850p:plain:w500

反対に、ベクトルを行列に戻す場合は以下のようなコードを書く。
f:id:sasakino:20200926094037p:plain:w430

Gradient Checking

逆伝搬の実装は複雑でバグが混入しやすい。
そして一見すると正しく動いているように見えてしまう。

この問題は、Gradient Checkingと呼ばれるアイデアで対処可能。
これは、別の方法で勾配(あるいはその近似値)を計算して、両者を比較することで正しさを検証するというもの。

勾配の近似値は下図のような式で求めることができる。
f:id:sasakino:20200926103112p:plain:w550

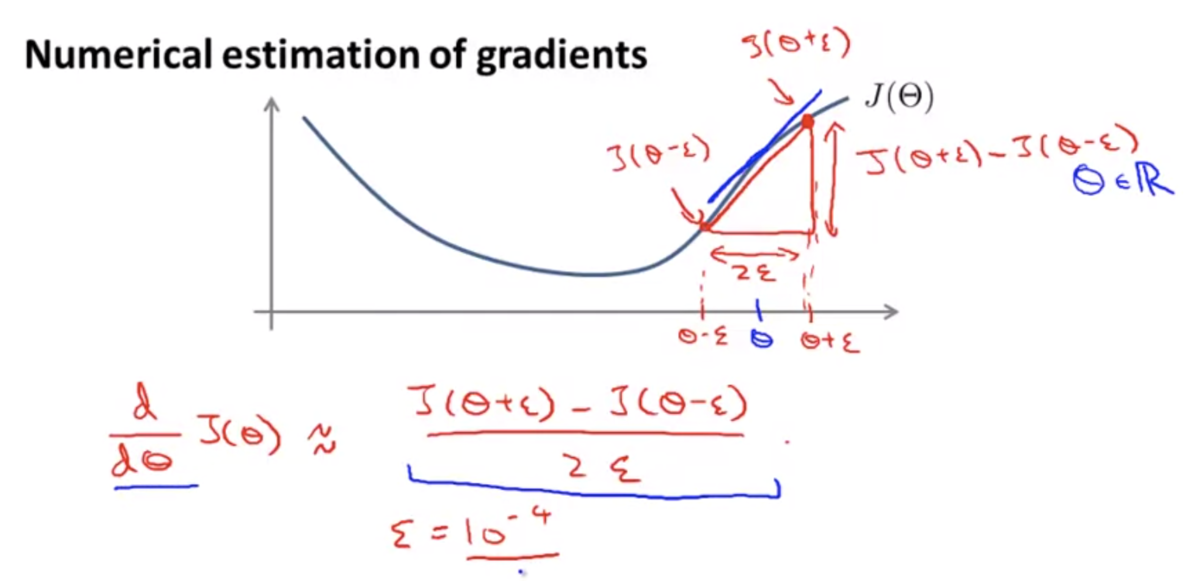
ある程度小さなεを設定し、これを使ってΘを両側微分したものを近似値として利用する。

Octaveで実装すると以下のようなコードになる。
f:id:sasakino:20200926103422p:plain:w550

Θをベクトルに拡張すると次のようになる。
f:id:sasakino:20200926103519p:plain:w500

Octaveで実装した場合こうなる。
f:id:sasakino:20200926103609p:plain

得られたgradApproxと逆伝搬の計算で得られたDVecを比較し、差がある範囲に収まれば、逆伝搬の計算は正しい可能性が高くなる。

なお、Gradient Checkingは逆伝搬の実装を検証する際にのみ使用し、実際に学習する際にはいちいち計算しないように注意する。

逆伝搬の計算と比較して計算に時間がかかるので、この方法を使って学習することはしない。

Random Initialization

Random Initializationと呼ばれるアイデアについて。

学習のために最適化アルゴリズムを走らせる際、パラメータΘの初期値を選ぶ必要がある。

ロジスティック回帰の場合は、ゼロ初期化でうまくいった。

しかしニューラルネットワークの場合、Θをゼロ初期化するとうまく動かない。
f:id:sasakino:20200926134512p:plain:w350

そのため、Θをランダムに初期化する必要がある。

Θを $-ε ≦ Θ _ {ij} ^ {(l)} ≦ ε$ の範囲の値で初期化するために、Octaveでは以下のように記述すればよい。

Theta1 = rand(10, 11) * (2 * INIT_EPSILON) - INIT_EPSILON;

Theta2 = rand(1, 11) * (2 * INIT_EPSILON) - INIT_EPSILON;

rand(10, 11)は10x11の0から1の間の値をとる行列を生成する。

Putting It Together

ニューラルネットワークの利用手順について。

● モデル形状の決定

入力層のユニット数 ... 扱う特徴量の数できまる
出力層のユニット数 ... 分類に必要なクラスの数できまる
隠れ層の数 ... 通常は1層でいい
隠れ層のユニット数 ... だいたい入力層のユニット数と同程度 ~ 4倍程度にする　隠れ層が複数あるなら各層のユニット数は同じにする

● 学習の実装

パラメータΘをランダムに初期化する (Θは0付近の値)
フォワードプロパゲーションを実装して $x ^ (i)$ に対する $h _ Θ (x ^ {(i)})$ を計算可能にする
コスト関数 $J(Θ)$ の実装
バックプロパゲーションを実装して偏微分 $\displaystyle{{\frac{∂}{∂Θ _ {jk} ^ {(l)}}J(Θ)}}$ を計算可能にする
バックプロパゲーションの実装の正しさを検証するためにGradient Checkingを行う (検証が済んだらこの処理はOFFにしておく)
勾配降下法、またはより高度な最適化アルゴリズムによって $J(Θ)$ を最小化する処理を実装する

Application of Neural Networks

Autonomous Driving

ニューラルネットワークで自動運転する研究結果の映像。

ささきのブログ

日記、技術メモ、勉強記録など。